
【题目】在平面直角坐标系中,以坐标原点为中心,以坐标轴为对称轴的帮圆C经过点M(2,1),N .
.
(1)求椭圆C的标准方程;
(2)经过点M作倾斜角互补的两条直线,分别与椭圆C相交于异于M点的A,B两点,当△AMB面积取得最大值时,求直线AB的方程.
【答案】(1)![]()
(2)![]() 或
或![]()
【解析】
(1)设椭圆C的方程为![]() (
(![]() ,
,![]() ,
,![]() ).
).
根据椭圆过![]() 两点,代入得到方程组,解得.
两点,代入得到方程组,解得.
(2)由直线AM,BM,AB的斜率存在,故.设它们的斜率分别为![]() ,
,![]() ,k.
,k.
设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]() .联立直线与椭圆方程,消元列出韦达定理,由
.联立直线与椭圆方程,消元列出韦达定理,由![]() .即
.即![]() . 即可解得
. 即可解得![]() ,或
,或![]() .分别代入检验,再用弦长公式及点到直线的距离公式,表示出三角形的面积,利用基本不等式求最值.
.分别代入检验,再用弦长公式及点到直线的距离公式,表示出三角形的面积,利用基本不等式求最值.
解:(1)设椭圆C的方程为![]() (
(![]() ,
,![]() ,
,![]() ).
).
∵点![]() 和N
和N 在椭圆C上,
在椭圆C上,
∴ .解得
.解得 .
.
∴椭圆C的标准方程为![]() .
.
(2)∵点A,B为椭圆上异于M的两点,且直线AM,BM的倾斜角互补,
∴直线AM,BM,AB的斜率存在.设它们的斜率分别为![]() ,
,![]() ,k.
,k.
设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]() .
.
∴![]() .
.
∴![]() .
.
由 ,消去y,得
,消去y,得![]() .
.
由![]() ,得
,得![]() .
.
∴![]() ,
,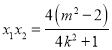 .
.
∴ .
.
∴![]() .
.
∴![]() .
.
∴![]() ,或
,或![]() .
.
∵点A,B为椭圆上异于M的两点,
∴当![]() 时,直线AB的方程为
时,直线AB的方程为![]() ,不合题意,舍去.
,不合题意,舍去.
∴直线AB的斜率为![]() .
.
∵![]() ,点M到直线AB的距离为
,点M到直线AB的距离为![]() ,
,
∴![]() 的面积为
的面积为![]() .
.
当且仅当![]() 时,
时,![]() 的面积取得最大值,此时
的面积取得最大值,此时![]() .
.
∵![]() ,
,![]() 满足
满足![]() .
.
∴直线AB的方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的右焦点为F(2,0),过点F的直线交椭圆于M、N两点且MN的中点坐标为
的右焦点为F(2,0),过点F的直线交椭圆于M、N两点且MN的中点坐标为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l不经过点P(0,b)且与C相交于A,B两点,若直线PA与直线PB的斜率的和为1,试判断直线 l是否经过定点,若经过定点,请求出该定点;若不经过定点,请给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙、丁、戌5人参加社区志愿者服务活动,每人从事团购、体温测量、进出人员信息登记、司机四项工作之一,每项工作至少有一人参加.若甲、乙不会开车但能从事其他三项工作,丙、丁、戌都能胜任四项工作,则不同安排方案的种数是( )
A.234B.152C.126D.108
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从甲地到乙地的公路里程约为240(单位:km).某汽车每小时耗油量Q(单位:L)与速度x(单位:![]() )(
)(![]() )的关系近似符合以下两种函数模型中的一种(假定速度大小恒定):①
)的关系近似符合以下两种函数模型中的一种(假定速度大小恒定):①![]() ,②
,②![]() ,经多次检验得到以下一组数据:
,经多次检验得到以下一组数据:
x | 0 | 40 | 60 | 120 |
Q | 0 |
|
| 20 |
(1)你认为哪一个是符合实际的函数模型,请说明理由;
(2)从甲地到乙地,这辆车应以多少速度行驶才能使总耗油量最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的体积为1.在侧棱
的体积为1.在侧棱![]() 上取一点
上取一点![]() ,使
,使![]() ,然后在
,然后在![]() 上取一点
上取一点![]() ,使
,使![]() ,继续在
,继续在![]() 上取一点
上取一点![]() ,使
,使![]() ,……按上述步骤,依次得到点
,……按上述步骤,依次得到点![]() ,记三棱锥
,记三棱锥![]() 的体积依次构成数列
的体积依次构成数列![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() .
.

(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)记![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,若不等式
项和,若不等式![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数![]() 满足
满足![]() ,则称
,则称![]() 为
为![]() 的不动点.已知函数
的不动点.已知函数
![]() ,其中,
,其中,![]() 、
、![]() 为常数。
为常数。
(1)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() 时,存在一个实数
时,存在一个实数![]() ,使得
,使得![]() 既是
既是![]() 的不动点,又是
的不动点,又是![]() 的极值点,求实数
的极值点,求实数![]() 的值;
的值;
(3)证明:不存在实数组![]() ,使得
,使得![]() 互异的两个极值点均为不动点.
互异的两个极值点均为不动点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年国庆黄金周旅游市场依旧火爆.一旅行社为某旅行团包机旅游,其中旅行社的包机费15000元,旅行团中每人的飞机票按以下方式与旅行社结算:若旅行团人数不超过35人,飞机票每张800元;若旅行团人数多于35人,则给予如下优惠:每多1人,每张机票减少10元,但旅行团的人数最多不超过60人,记旅行团人数为![]() ,每个人的机票钱为y元.
,每个人的机票钱为y元.
(1)写出![]() 与
与![]() 的关系式.
的关系式.
(2)求旅行社获得的利润![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R.若存在与x无关的正常数M,使|f(x)|≤ M|x|对一切实数x均成立,则称f(x)为有界泛函.则函数:① f(x)=-3x,② f(x)=x2,③ f(x)=sin2x,④ f(x)=2x,⑤ f(x)=xcosx中,属于有界泛函的有____________.(填上所有正确的番号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是古希腊数学家阿基米德用平衡法求球的体积所用的图形.此图由正方形![]() 、半径为
、半径为![]() 的圆及等腰直角三角形构成,其中圆内切于正方形,等腰三角形的直角顶点与
的圆及等腰直角三角形构成,其中圆内切于正方形,等腰三角形的直角顶点与![]() 的中点
的中点![]() 重合,斜边在直线
重合,斜边在直线![]() 上.已知
上.已知![]() 为
为![]() 的中点,现将该图形绕直线
的中点,现将该图形绕直线![]() 旋转一周,则阴影部分旋转后形成的几何体积为( )
旋转一周,则阴影部分旋转后形成的几何体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com