
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 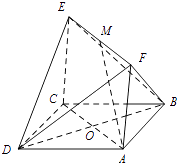
(1)求证:AM∥平面BDE;
(2)求证:AM⊥平面BDF;
(3)求A点到面BDF的距离.
【答案】
(1)证明:设底面对角线的交点为O,连接EO.
∵M为EF的中点,四边形ACEF为矩形
∴EM∥AO且EM=AO
∴AM∥OE
又因为OE平面BDE 且AM平面BDE
∴AE∥平面BDE.
(2)证明:设AC与BD交于O点,连OF,OM
在矩形ACEF中四边形, ![]() ,AF=1
,AF=1
所以,AOMF为正方形,故AM⊥OF
又正方形ABCD和矩形ACEF所在的平面互相垂直,且交线为AC
在正方形ABCD中,故AC⊥BD
由面面垂直的性质定理,BD⊥面ACEF
又AM面ACEF
所以BD⊥AM
又BD∩OF=O,故AM⊥平面BDF

(3)解:VA﹣BDF=VF﹣ABD,设A到面BDF的距离为h,∴ ![]()
∴ ![]()
【解析】(1)证明四边形AMEN是平行四边形,可得AM∥OE,OE在平面BDE面内,AM在平面BDE面外,满足线面平行的判定定理所需条件,从而证得结论;(2)证明AC⊥BD,BD⊥AM,又BD∩OF=O,即可证明AM⊥平面BDF;(3)利用VA﹣BDF=VF﹣ABD , 求出A到面BDF的距离.
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.


科目:高中数学 来源: 题型:
【题目】我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知F1、F2是一对相关曲线的焦点,P是它们在第一象限的交点,当∠F1PF2=60°时,这一对相关曲线中双曲线的离心率是( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,动点P在底面ABCD内,且P到棱AD的距离与到面对角线BC1的距离相等,则点P的轨迹是( )
A.线段
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AC⊥BC,AB⊥BB1 , AC=BC=BB1 , D为AB的中点,且CD⊥DA1 . 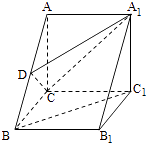
(1)求证:BC1∥平面DCA1;
(2)求BC1与平面ABB1A1所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com