
【题目】函数![]() .
.
(1)当![]() 时,求方程
时,求方程![]() 的根的个数;
的根的个数;
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
注:![]() 为自然对数的底数
为自然对数的底数
【答案】(1)两个 (2)![]()
【解析】
(1)转化为研究函数![]() 零点问题,利用导数研究其单调性,再根据零点存在定理确定零点个数;
零点问题,利用导数研究其单调性,再根据零点存在定理确定零点个数;
(2)先转化为对应函数最值问题:![]() ,再令
,再令![]() ,转化为解不等式
,转化为解不等式![]() ,最后根据导数研究新函数单调性,根据单调性解不等式得结果.
,最后根据导数研究新函数单调性,根据单调性解不等式得结果.
(1)当![]() 时,构造函数
时,构造函数![]() ,求导得:
,求导得: ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
∵![]() .
.
又∵![]() ,
,
∴![]() ,使
,使![]() ,即
,即![]() 存在两个零点
存在两个零点![]() ,
,
∴方程![]() 存在两个根.
存在两个根.
(2) ,
,
i)当![]() 时,
时,![]() ,不合题意,舍去;
,不合题意,舍去;
ii)当![]() 时,由
时,由![]() 可得
可得![]() ,列表:
,列表:
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
据表可得,![]() ,依题意有
,依题意有![]()
令![]() ,则上式等价于
,则上式等价于![]() ,等价于
,等价于![]() ,
,
构造函数![]() ,
,
记函数![]() ,易证得
,易证得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上单调递增,注意到
上单调递增,注意到![]() ,
,
∴![]() .
.
综上所述,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在一条景观道的一端有一个半径为![]() 米的圆形摩天轮O,逆时针
米的圆形摩天轮O,逆时针![]() 分钟转一圈,从
分钟转一圈,从![]() 处进入摩天轮的座舱,
处进入摩天轮的座舱,![]() 垂直于地面
垂直于地面![]() ,在距离
,在距离![]() 处
处![]() 米处设置了一个望远镜
米处设置了一个望远镜![]() .
.

(1)同学甲打算独自乘坐摩天轮,但是其母亲不放心,于是约定在登上摩天轮座舱![]() 分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜
分钟后,在座舱内向其母亲挥手致意,而其母亲则在望远镜![]() 中仔细观看.问望远镜
中仔细观看.问望远镜![]() 的仰角
的仰角![]() 应调整为多少度?(精确到1度)
应调整为多少度?(精确到1度)
(2)在同学甲向其母亲挥手致意的同时,同一座舱的另一名乘客乙在拍摄地面上的一条绿化带![]() ,发现取景的视角
,发现取景的视角![]() 恰为
恰为![]() ,求绿化带
,求绿化带![]() 的长度(精确到1米)
的长度(精确到1米)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为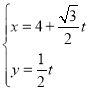 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)在曲线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,求
,求![]() 点轨迹的极坐标方程;
点轨迹的极坐标方程;
(2)在曲线![]() 上任取一点
上任取一点![]() ,在曲线
,在曲线![]() 上任取一点
上任取一点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别是椭圆的左右焦点,过点
分别是椭圆的左右焦点,过点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,且
两点,且![]() 的周长为12.
的周长为12.
(Ⅰ)求椭圆![]() 的方程
的方程
(Ⅱ)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
,![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形若存在,求点
为底边的等腰三角形若存在,求点![]() 横坐标的取值范围,若不存在,请说明理由.
横坐标的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
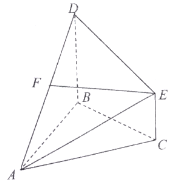
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,平面
,平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.
(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
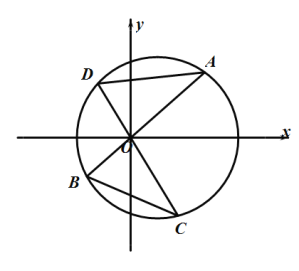
【题目】已知圆![]() ,线段
,线段![]() 、
、![]() 都是圆
都是圆![]() 的弦,且
的弦,且![]() 与
与![]() 垂直且相交于坐标原点
垂直且相交于坐标原点![]() ,如图所示,设△
,如图所示,设△![]() 的面积为
的面积为![]() ,设△
,设△![]() 的面积为
的面积为![]() .
.
(1)设点![]() 的横坐标为
的横坐标为![]() ,用
,用![]() 表示
表示![]() ;
;
(2)求证:![]() 为定值;
为定值;
(3)用![]() 、
、![]() 、
、![]() 、
、![]() 表示出
表示出![]() ,试研究
,试研究![]() 是否有最小值,如果有,求出最小值,并写出此时直线
是否有最小值,如果有,求出最小值,并写出此时直线![]() 的方程;若没有最小值,请说明理由.
的方程;若没有最小值,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com