
【题目】选修4-5:不等式选讲
已知![]() ,且
,且![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)求![]() 的最大值.
的最大值.
【答案】(1)8;(2)![]() .
.
【解析】试题分析: (Ⅰ)根据题中等式由基本不等式放缩,可得![]() 的范围,再由
的范围,再由![]() 可得最小值; (Ⅱ)结合要求的最值可得
可得最小值; (Ⅱ)结合要求的最值可得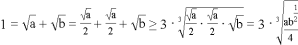 ,所以
,所以![]() ,验证取等条件求出最值.
,验证取等条件求出最值.
试题解析:(Ⅰ)由![]() ,可得
,可得![]() ,
,
![]() ,
,
当且仅当![]() 时等号成立,因此
时等号成立,因此![]() 的最小值为8.
的最小值为8.
(Ⅱ)因为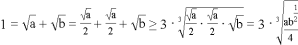 ,
,
所以![]() ,
,
当且仅当![]() ,即
,即![]() 且
且![]() 时,等号成立.
时,等号成立.
点睛:本题考查学生利用基本不等式与和或者乘积的定值求最值的问题,属于中档题目. 解此类题目的两个技巧: (1)创设运用基本不等式的条件,合理拆分项或配凑因式,其目的在于使等号能够成立.(2)既要记住基本不等式的原始形式,而且还要掌握它的变形形式及公式的逆用等,例如:ab≤![]() 2≤
2≤![]() ,
,![]() ≤
≤![]() ≤
≤ ![]() (a>0,b>0).
(a>0,b>0).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】据报道,巴基斯坦由中方投资运营的瓜达尔港目前已通航.这是一个可以停靠8![]() 10万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约340亿美元,公路投资约59亿美元,铁路投资约38亿美元,高架铁路投资约16亿美元,瓜达尔港投资约6.6亿美元,光纤通讯投资约为0.4亿美元.
10万吨油轮的深水港,通过这一港口,中国船只能够更快到达中东和波斯湾地区,这相当于给中国平添了一条大动脉!在打造中巴经济走廊协议(简称协议)中,能源投资约340亿美元,公路投资约59亿美元,铁路投资约38亿美元,高架铁路投资约16亿美元,瓜达尔港投资约6.6亿美元,光纤通讯投资约为0.4亿美元.
有消息称,瓜达尔港的月货物吞吐量将是目前天津、上海两港口月货物吞吐量之和.表格记录了2015年天津、上海两港口的月吞吐量(单位:百万吨):
1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
天津 | 24 | 22 | 26 | 23 | 24 | 26 | 27 | 25 | 28 | 24 | 25 | 26 |
上海 | 32 | 27 | 33 | 31 | 30 | 31 | 32 | 33 | 30 | 32 | 30 | 30 |
(Ⅰ)根据协议提供信息,用数据说明本次协议投资重点;
(Ⅱ)从表中12个月任选一个月,求该月天津、上海两港口月吞吐量之和超过55百万吨的概率;
(Ⅲ)将(Ⅱ)中的计算结果视为瓜达尔港每个月货物吞吐量超过55百万吨的概率,设![]() 为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出
为瓜达尔未来12个月的月货物吞吐量超过55百万吨的个数,写出![]() 的数学期望(不需要计算过程).
的数学期望(不需要计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某金匠以黄金为原材料加工一种饰品,经多年的数据统计得知,该金匠平均每加5 个饰品中有4个成品和1个废品,每个成品可获利3万元,每个废品损失1万元,假设该金匠加工每件饰品互不影响,以频率估计概率.
(1)若金金匠加工4个饰品,求其中废品的数量不超过1的概率;
(2)若该金匠加工了 3个饰品,求他所获利润的数学期望.
(两小问的计算结果都用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即S= ![]() .现有周长为2
.现有周长为2 ![]() +
+ ![]() 的△ABC满足sinA:sinB:sinC=(
的△ABC满足sinA:sinB:sinC=( ![]() ﹣1):
﹣1): ![]() :(
:( ![]() +1),试用以上给出的公式求得△ABC的面积为( )
+1),试用以上给出的公式求得△ABC的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若奇函数y=f(x)在区间(0,+∞)上是增函数,又f(﹣3)=0,则不等式f(x)<0的解集为( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(0,3)
D.(﹣∞,﹣3)∪(3,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com