【答案】
分析:(1)分别求出集合A和集合B中的不等式的解集,然后求出两集合的交集即可;
(2)由题意和(1)中的结论可知-3和1为方程的两个根,把-3和1分别代入方程中得到关于a与b的方程,求出方程的解即可得到a与b的值.
解答:解:(1)A={x|x
2<4}={x|-2<x<2},B=
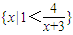
={x|-3<x<1},
∴A∩B={x|-2<x<1};
(2)由题意及(1)有-3,1是方程2x
2+ax+b=0的两根
∴
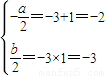
∴
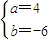
.
点评:此题属于以不等式的解集为平台,考查了交集的运算,同时要求学生掌握一元二次方程的根的分布与系数的关系,是一道综合题.

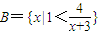 .
. 每课必练系列答案
每课必练系列答案