
����Ŀ��ij�ۿڴ���ͣ���ķ������ȵ���ͣ��
��1�����������Ҵ�ͬʱ����ۿڣ�˫��Լ������һ��������ȭ����1��2,3��4,5�и����ѡһ������������֮��Ϊż���������ͣ����������֮��Ϊ������������ͣ�������ֹ����Ƿ�ƽ����˵�����ɣ�
��2�������������飬�״���������![]() ����Ҵ���������
����Ҵ���������![]() �����Ӧ�����ģ��ķ�����״���ͣ���ĸ��ʣ������ģ��ʵ�����ݲο����£���
�����Ӧ�����ģ��ķ�����״���ͣ���ĸ��ʣ������ģ��ʵ�����ݲο����£���![]() ��
�� ![]() ����
����![]() ֮��ľ�����������ü��������100�����飬�õ��Ľ����12������
֮��ľ�����������ü��������100�����飬�õ��Ľ����12������![]() ����6������
����6������![]() ��
��
���𰸡���1������ƽ��2��0.88
�����������������
(1)���ùŵ���ͼ��㹫ʽ����������ʤΪ�¼�![]() ����ʤΪ�¼�
����ʤΪ�¼�![]() ������ɵü�ʤ�ĸ���
������ɵü�ʤ�ĸ���![]() ����ʤ�ĸ���
����ʤ�ĸ���![]() ����������Ϸ����ƽ��
����������Ϸ����ƽ��
(2) Ӧ�����ģ��ķ��������![]() ����״���ͣ�����������⣬100��������12�ν������
����״���ͣ�����������⣬100��������12�ν������![]() ����״���ͣ���ĸ�����
����״���ͣ���ĸ�����![]() ��
��
���������
��1�����ֹ����Dz���ƽ�ģ�
���ʤΪ�¼�![]() ����ʤΪ�¼�
����ʤΪ�¼�![]() �������¼�����Ϊ
�������¼�����Ϊ![]() �֣�
�֣�
���ʤ������ź�Ϊż���������Ļ����¼�����13���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ��
��
���ʤ�ĸ���![]() ����ʤ�ĸ���
����ʤ�ĸ���![]() ��
��
��������Ϸ����ƽ��
��2��Ӧ�����ģ��ķ��������![]() ����
����![]() ����״���ͣ����
����״���ͣ����
�������⣬100��������12�ν������![]() ��
��
���Լ״���ͣ���ĸ�����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ԭ�㣬������x���ϵ�һ��Բ��һ˫�����й�ͬ�Ľ���F1��F2����|F1F2|��![]() ����Բ�ij�������˫����ʵ����֮��Ϊ4��������֮��Ϊ3��7.
����Բ�ij�������˫����ʵ����֮��Ϊ4��������֮��Ϊ3��7.
��1�����������ߵķ��̣�
��2����PΪ�������ߵ�һ�����㣬��cos��F1PF2��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p��ʵ��x����x2-5ax+4a2��0������a��0������q��ʵ��x����![]() ��
��
��1����a=1����p��qΪ�棬��ʵ��x��ȡֵ��Χ��
��2�����Vp�ǩVq�ij�ֲ���Ҫ��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г����飬ij���е�һ��С��Ʒ�ڹ�ȥ�Ľ�20���ڵ���������������۸�Ԫ����Ϊʱ��t���죩�ĺ���������������������g��t��=80��2t���������۸����������  ��Ԫ����
��Ԫ����
��1����д��������Ʒ�������۶�y��ʱ��t��0��t��20���ĺ�������ʽ��
��2���������Ʒ�������۶�y�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������˵����
�����⡰![]() ��Ϊ�٣���
��Ϊ�٣���![]() ��
��![]() ����һ��Ϊ�٣�
����һ��Ϊ�٣�
�����⡰һ�κ������ǵ����������ķ��ǡ�һ�κ��������ǵ�����������
�۶���![]() ����
����![]()
![]() �뵽��
�뵽��![]() �ľ���֮��Ϊ2�����
�ľ���֮��Ϊ2�����![]() �Ĺ켣�ǽ�����
�Ĺ켣�ǽ�����![]() ���ϵ���Բ��
���ϵ���Բ��
�����⡰��ֱ����˫�������У����ֱ����˫����ֻ��һ�������㡱���������������⣮
������ȷ����__________������д��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ![]() ��������Ϊ
��������Ϊ![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��

��1������Բ![]() �ķ��̣�
�ķ��̣�
��2��![]() ����Բ
����Բ![]() �ϳ������������㣬ֱ��
�ϳ������������㣬ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��б��Ϊ
��б��Ϊ![]() ��
�� ![]() ��б��Ϊ
��б��Ϊ![]() ������
������![]() �Ƿ�Ϊ��ֵ����˵�����ɣ�
�Ƿ�Ϊ��ֵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ڶ���P��x��y����������A��-2, 0��, B��2,0�����ߵ�б��֮������![]() ������P�Ĺ켣Ϊ����E������Q
������P�Ĺ켣Ϊ����E������Q![]() ��б�ʲ�Ϊ���ֱ��
��б�ʲ�Ϊ���ֱ��![]() ������E�ڵ�
������E�ڵ�![]() ��
��
��I��������E�ķ�����
��II����֤�� ![]() ��
��
��III����![]() ��������ֵ��
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
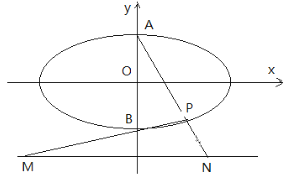
����Ŀ����ͼ��Բ![]() �����¶���ΪA��B��ֱ��
�����¶���ΪA��B��ֱ��![]() ��
�� ![]() ����P����Բ�����ڵ�A��B������һ�㣬����AP���ӳ���ֱ��
����P����Բ�����ڵ�A��B������һ�㣬����AP���ӳ���ֱ��![]() �ڵ�N������BP���ӳ���ֱ��
�ڵ�N������BP���ӳ���ֱ��![]() �ڵ�M����AP��BP����ֱ�ߵ�б�ʷֱ�Ϊ
�ڵ�M����AP��BP����ֱ�ߵ�б�ʷֱ�Ϊ![]() ������Բ��������Ϊ
������Բ��������Ϊ![]() ���ҹ���
���ҹ���![]() ����1����
����1����![]() ��ֵ������
��ֵ������![]() ��Сֵ����2�����ŵ�P�ı仯����MNΪֱ����Բ�Ƿ������㣬�������㣬����ö������ꣻ���������㣬��˵�����ɡ�
��Сֵ����2�����ŵ�P�ı仯����MNΪֱ����Բ�Ƿ������㣬�������㣬����ö������ꣻ���������㣬��˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��������800��ѧ����Ϊ�˽�ѧ��3���¿�������������������Ůѧ����������ϴ��������ȡ��200��ѧ������¼���ǵķ���������������ͼƵ�ʷֲ�ֱ��ͼ��
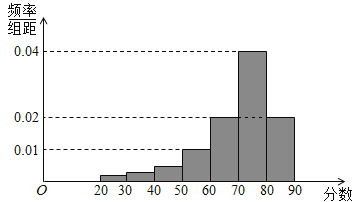
��1�����ɼ�������60�ֵ�Ϊ���ɼ�������80�ֵ�Ϊ���㣬�Թ��������кϸ���ж����ˣ�������ж����ˣ�
��2����֪��������һ���Ů��������С��80���������в�����80�ֵ���Ů������֮��2:3���Թ���������������Ů�������ı�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com