
| A. | (0,$\sqrt{2}$) | B. | (0,$\sqrt{2}$)∪(4,+∞) | C. | (0,2) | D. | (0,2)∪(16,+∞) |
分析 先根据“设min{p,q}表示p,q两者中的较小的一个”求得函数f(x),再按分段函数用分类讨论解不等式.
解答 解:①当3-$\frac{1}{2}$log2x<log2x时,
即 x>4时f(x)=3-$\frac{1}{2}$log2x,
②当3-$\frac{1}{2}$log2x>log2x时,
即x<4时f(x)=log2x,
∴f(x)<1;
当x>4时,
f(x)=3-$\frac{1}{2}$log2x<1,
此时:x>16;
当x<4时f(x)=log2x<1,
此时:0<x<2;
综上不等式的解集为:(0,2)∪(16,+∞).
故选:D.
点评 本题是一道新定义题,首先要根据定义求得函数,再应用函数解决相关问题,这类问题的解决,正确转化是关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω>0,π<φ<$\frac{3π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
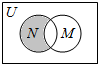 设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.
设全集U是实数集R,M={x|x2>4},N={x|$\frac{2}{x-1}$≥1},则图中阴影部分所表示集合是{x|1<x≤2}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,0)∪($\frac{1}{2}$,+∞) | B. | (-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) | C. | (-∞,-$\frac{1}{2}$)∪(0,$\frac{1}{2}$) | D. | (-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com