
【题目】已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)将方程化为标准式方程,可得到圆心坐标;(2)设线段![]() 的中点,
的中点,![]() 直线
直线![]() 的方程为
的方程为![]() 联立直线和圆的方程得到韦达定理,进而得到
联立直线和圆的方程得到韦达定理,进而得到![]() ,
,![]() ,此时消去参数m即可得到轨迹方程;(3)结合第二问可得到曲线的轨迹,根据直线和圆的位置关系可得到满足题意的结果.
,此时消去参数m即可得到轨迹方程;(3)结合第二问可得到曲线的轨迹,根据直线和圆的位置关系可得到满足题意的结果.
(1)圆![]()
![]() 化为
化为![]() ,所以圆
,所以圆![]() 的圆心坐标为
的圆心坐标为![]()
(2)设线段![]() 的中点,
的中点,![]() 直线
直线![]() 的方程为
的方程为![]() (易知直线
(易知直线![]() 的斜率存在),则
的斜率存在),则![]() 得:
得:![]()
![]() .解得:
.解得:![]()
![]()
![]()
![]() 消去
消去![]() 得:
得:![]()
又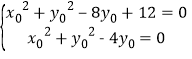 解得:
解得:![]() 或
或![]()
![]()
![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
(3)由题意知直线![]() 表示过定点
表示过定点![]()
![]() ,斜率为
,斜率为![]() 的直线.
的直线.
![]() 表示的是一段关于
表示的是一段关于![]() 轴对称,起点为
轴对称,起点为![]() 按顺时针方向运动到
按顺时针方向运动到![]() 的圆弧(不包含端点
的圆弧(不包含端点![]() ).
).
由条件得:![]() 而当直线
而当直线![]() 与轨迹
与轨迹![]() 相切时,
相切时,![]() ,解得
,解得![]() (舍去).
(舍去).
可得当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 只有一个交点。
只有一个交点。
综上所述,当时![]() 直线
直线![]()
![]() 与曲线
与曲线![]() 只有一个交点.
只有一个交点.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数),将曲线C1上所有点的横坐标缩短为原来的
(α为参数),将曲线C1上所有点的横坐标缩短为原来的 ![]() ,纵坐标缩短为原来的
,纵坐标缩短为原来的 ![]() ,得到曲线C2 , 在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为4ρsin(θ+
,得到曲线C2 , 在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为4ρsin(θ+ ![]() )+
)+ ![]() =0.
=0.
(1)求曲线C2的极坐标方程及直线l与曲线C2交点的极坐标;
(2)设点P为曲线C1上的任意一点,求点P到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是自动通风设施![]() 该设施的下部ABCD是等腰梯形,其中
该设施的下部ABCD是等腰梯形,其中![]() 米,高
米,高![]() 米,
米,![]() 米
米![]() 上部CmD是个半圆,固定点E为CD的中点
上部CmD是个半圆,固定点E为CD的中点![]() 是由电脑控制其形状变化的三角通风窗
是由电脑控制其形状变化的三角通风窗![]() 阴影部分均不通风
阴影部分均不通风![]() ,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
,MN是可以沿设施边框上下滑动且始终保持和CD平行的伸缩横杆.
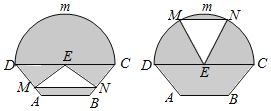
![]() 设MN与AB之间的距离为x米,试将三角通风窗
设MN与AB之间的距离为x米,试将三角通风窗![]() 的通风面积
的通风面积![]() 平方米
平方米![]() 表示成关于x的函数
表示成关于x的函数![]() ;
;
![]() 当MN与AB之间的距离为多少米时,三角通风窗
当MN与AB之间的距离为多少米时,三角通风窗![]() 的通风面积最大?求出这个最大面积.
的通风面积最大?求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为2的正方体![]() 沿对角线
沿对角线![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,则下列命题中,错误的为( )
,则下列命题中,错误的为( )
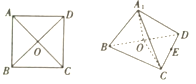
A. 直线![]() 平面
平面![]()
B. ![]()
C. 三棱锥![]() 的外接球的半径为
的外接球的半径为![]()
D. 若![]() 为
为![]() 的中点,则
的中点,则![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合M={1,2…9}中抽取3个不同的数构成集合{a1 , a2 , a3}
(1)对任意i≠j,求满足|ai﹣aj|≥2的概率;
(2)若a1 , a2 , a3成等差数列,设公差为ξ(ξ>0),求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系xOy中,直线l的参数方程为 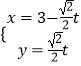 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程和直线l普通方程;
(2)设圆C与直线l交于点A,B,若点P的坐标为(3,0),求|PA|+|PB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com