
【题目】物联网兴起、发展、完善极大的方便了市民生活需求.某市统计局随机地调查了该市某社区的100名市民网上购菜状况,其数据如下:
每周网上买菜次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 | 总计 |
男 | 10 | 8 | 7 | 3 | 2 | 15 | 45 |
女 | 5 | 4 | 6 | 4 | 6 | 30 | 55 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 | 100 |
(1)把每周网上买菜次数超过3次的用户称为“网上买菜热爱者”,能否在犯错误概率不超过0.005的前提下,认为是否为“网上买菜热爱者”与性别有关?
(2)把每周使用移动支付6次及6次以上的用户称为“网上买菜达人”,视频率为概率,在我市所有“网上买菜达人”中,随机抽取4名用户求既有男“网上买菜达人”又有女“网上买菜达人”的概率.
附公式及表如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)在犯错误概率不超过0.005的前提下,能认为是否为“网上买菜热爱者”与性别有关(2)![]()
【解析】
(1)根据题意列出![]() 列联表,由公式计算
列联表,由公式计算![]() ,再由给出的对照表进行比较,得出结论.
,再由给出的对照表进行比较,得出结论.
(2)由题意可得随机抽取1名用户,该用户为男“移动支付达人”的概率为![]() ,女移动支付达人“的概率为
,女移动支付达人“的概率为![]() ,然后求出抽取的4名用户中,全为男“移动支付达人”的概率和抽取的4名用户中,全为女“移动支付达人”的概率,再由对立事件的概率可求出答案.
,然后求出抽取的4名用户中,全为男“移动支付达人”的概率和抽取的4名用户中,全为女“移动支付达人”的概率,再由对立事件的概率可求出答案.
(1)由表格数据可得![]() 列联表如下:
列联表如下:
非移动支付活跃用户 | 移动支付活跃用户 | 合计 | |
男 | 25 | 20 | 45 |
女 | 15 | 40 | 55 |
合计 | 40 | 60 | 100 |
将列联表中的数据代入公式计算得:
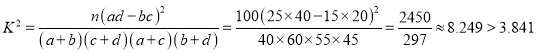 ,
,
所以在犯错误概率不超过0.005的前提下,能认为是否为“网上买菜热爱者”与性别有关.
(2)每周使用移动支付6次及6次以上的用户有45户.其中男性15户,女性30户.
视频率为概率,在我市“移动支付达人”中,随机抽取1名用户,
该用户为男“移动支付达人”的概率为![]() ,女移动支付达人“的概率为
,女移动支付达人“的概率为![]() .
.
抽取的4名用户中,全为男“移动支付达人”的概率为:![]()
抽取的4名用户中,全为女“移动支付达人”的概率为:![]()
抽取的4名用户中,既有男“移动支付达人”,又有女“移动支付达人”的概率为 .
.


科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左右焦点,点
的左右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 和
和![]() ,且
,且![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 等差数列?若存在,求出的值,若不存在,请说明理由.
等差数列?若存在,求出的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某地出土的一种“钉”是由四条线段组成,其结构能使它任意抛至水平面后,总有一端所在的直线竖直向上,并记组成该“钉”的四条线段的公共点为O,钉尖为![]() .
.
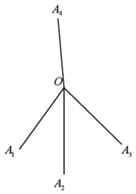
⑴设![]() ,当
,当![]() ,
,![]() ,
,![]() 在同一水平面内时,求
在同一水平面内时,求![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() 结果用反三角函数值表示
结果用反三角函数值表示![]() .
.
⑵若该“钉”的三个钉尖所确定的三角形的面积为![]() ,要用某种线型材料复制100枚这种“钉”
,要用某种线型材料复制100枚这种“钉”![]() 损耗忽略不计
损耗忽略不计![]() ,共需要该种材料多少米?
,共需要该种材料多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2016年到2019年的某城市方便面销量情况如图所示:
年份 | 2016 | 2017 | 2018 | 2019 |
时间代号 | 1 | 2 | 3 | 4 |
年销量 | 462 | 444 | 404 | 385 |
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2020年(
.用所求回归方程预测2020年(![]() )方便面在该城市的年销量;
)方便面在该城市的年销量;
(2)某媒体记者随机对身边的10位朋友做了一次调查,其中3位受访者认为方便面是健康食品.现从这10人中抽取3人进行深度访谈,记![]() 表示随机抽取的3人认为方便面是健康食品的人数,求随机变量
表示随机抽取的3人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中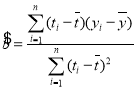 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中共有8个球,其中有3个白球,5个黑球,这些球除颜色外完全相同.从袋中随机取出一球,如果取出白球,则把它放回袋中;如果取出黑球,则该黑球不再放回,并且另补一个白球放入袋中.重复上述过程![]() 次后,袋中白球的个数记为
次后,袋中白球的个数记为![]() .
.
(1)求随机变量![]() 的概率分布及数学期望
的概率分布及数学期望![]() ;
;
(2)求随机变量![]() 的数学期望
的数学期望![]() 关于
关于![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,规定凡在该超市购物满400元的顾客,均可获得一次摸奖机会.摸奖规则如下:奖盒中放有除颜色不同外其余完全相同的4个球(红、黄、黑、白).顾客不放回的每次摸出1个球,若摸到黑球则摸奖停止,否则就继续摸球.按规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次摸奖停止的概率;
(2)记X为1名顾客摸奖获得的奖金数额,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com