
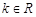 ,函数
,函数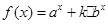
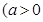 且
且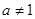 ,
,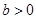 且
且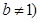 .
.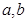 满足
满足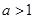 且
且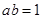 ,函数
,函数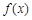 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的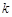 值;如果没有,说明原因;
值;如果没有,说明原因;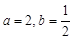 ,讨论函数
,讨论函数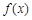 的单调性。
的单调性。科目:高中数学 来源:不详 题型:填空题
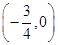 成中心对称,对任意实数x都有f(x)=-
成中心对称,对任意实数x都有f(x)=- ,且f(-1)=1,f(0)=-2,则f(0)+f(1)+…+f(2013)=________.
,且f(-1)=1,f(0)=-2,则f(0)+f(1)+…+f(2013)=________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
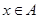 ,
,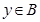 ,(
,(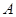 、
、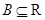 )有唯一确定的
)有唯一确定的 与之对应,称
与之对应,称 为关于
为关于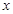 、
、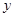 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数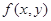 为关于实数
为关于实数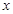 、
、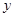 的广义“距离”:
的广义“距离”: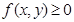 ,当且仅当
,当且仅当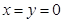 时取等号;
时取等号;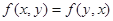 ;
;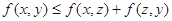 对任意的实数z均成立.
对任意的实数z均成立.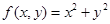 ;②
;②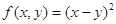 ;③
;③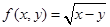 ;
;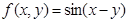 .能够成为关于的
.能够成为关于的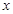 、
、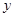 的广义“距离”的函数的所有序号是( )
的广义“距离”的函数的所有序号是( )| A.① | B.② | C.③ | D.④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com