
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() (a>0,且a≠1)的反函数为
(a>0,且a≠1)的反函数为![]() ,函数y=g(x)的图像与
,函数y=g(x)的图像与![]() 的图像关于点(a,0)对称。
的图像关于点(a,0)对称。
(1)求函数y=g(x)的解析式。
(2)是否存在实数a,使得当![]() 时,恒有
时,恒有![]() 成立?若存在,求出a的取值范围;若不存在,说明理由。
成立?若存在,求出a的取值范围;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如城镇小汽车的普及率为75%,即平均每100个家庭有75个家庭拥有小汽车,若从如城镇中任意选出5个家庭,则下列结论成立的是( )
A.这5个家庭均有小汽车的概率为![]()
B.这5个家庭中,恰有三个家庭拥有小汽车的概率为![]()
C.这5个家庭平均有3.75个家庭拥有小汽车
D.这5个家庭中,四个家庭以上(含四个家庭)拥有小汽车的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于简单几何体的说法中正确的是( )
①有两个面互相平行,其余各面都是平行四边形的多面体是棱柱;
②有一个面是多边形,其余各面都是三角形的几何体是棱锥;
③有两个底面平行且相似,其余各面都是梯形的多面体是棱台;
④空间中到定点的距离等于定长的所有点的集合是球面.
A.①②B.③④C.④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
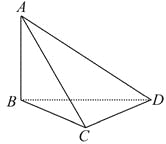
【题目】要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD="40" m,则电视塔的高度为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当m=1时,若方程![]() 在区间
在区间![]() 上有唯一的实数解,求实数a的取值范围;
上有唯一的实数解,求实数a的取值范围;
(3)当m>0时,若对于区间[1,2]上的任意两个实数x1,x2,且x1<x2,都有![]() 成立,求实数m的最大值.
成立,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边上有一点P的坐标是(3a,a),其中a≠0.
(1)求cos(α![]() )的值;
)的值;
(2)若tan(2α+β)=1,求tanβ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com