
【题目】已知函数f(x)= ![]() -
-![]() ,g(x)=
,g(x)= ![]() .
.
(1)若![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像相切,求
的图像相切,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 满足对任意
满足对任意![]() (x1
(x1![]() x2),都有
x2),都有![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() =f(x)+ g(x),且G(
=f(x)+ g(x),且G(![]() )有两个极值点x1,x2,其中x1
)有两个极值点x1,x2,其中x1![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)设切点为![]() ),则切线方程为
),则切线方程为![]() ,所以
,所以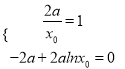 解方程组即可得结果;(2)不妨设
解方程组即可得结果;(2)不妨设![]() ,原不等式等价于
,原不等式等价于![]() .设
.设![]() ,则原不等式转化为
,则原不等式转化为![]() 在
在![]() 上递减,只需
上递减,只需![]() 在
在![]() 上恒成立即可;(3)
上恒成立即可;(3)![]() =
= ![]() ,
,![]() ,由题意知
,由题意知![]() 是
是![]() 的两根,利用韦达定理
的两根,利用韦达定理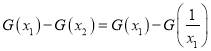
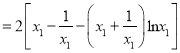 ,利用导数求出
,利用导数求出![]() =2
=2![]() 的最小值即可.
的最小值即可.
试题解析:(1)若b=0,函数f(x)=x的图像与g(x)=2alnx的图像相切,设切点为(x0,2alnx0),则切线方程为y=![]() ,所以
,所以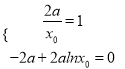 得
得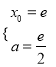 .所以a=
.所以a=![]() .
.
(2)当a>0,b=-1时,F(x)=x2+1+2alnx,F'(x)=2x+![]() >0,所以F(x)在(0,1]递增.
>0,所以F(x)在(0,1]递增.
不妨设0<x1<x2![]() 1,原不等式
1,原不等式![]() F(x2)-F(x1)<3(
F(x2)-F(x1)<3(![]() ),即F(x2)+
),即F(x2)+ ![]() < F(x1)+
< F(x1)+ ![]() .
.
设h(x)= F(x)+ ![]() = x2+1+2alnx+
= x2+1+2alnx+![]() ,则原不等式
,则原不等式![]() h(x)在(0,1]上递减
h(x)在(0,1]上递减
即h'(x)=2x+![]() -
-![]() 在(0,1]上恒成立.所以2a
在(0,1]上恒成立.所以2a![]() -2x2在(0,1]上恒成立.
-2x2在(0,1]上恒成立.
设y=![]() -2x2,在(0,1]上递减,所以ymin=3-2=1,所以2a
-2x2,在(0,1]上递减,所以ymin=3-2=1,所以2a![]() 1,又a>0,所以0<a
1,又a>0,所以0<a![]() .
.
(3)若b=1,函数G(x)=f(x)+g(x)=x![]() +2alnx
+2alnx
G/(x)= ![]() ,(x>0),由题意知x1,x2是x2+2ax+1=0的两根,
,(x>0),由题意知x1,x2是x2+2ax+1=0的两根,
∴x1x2=1, x1+x2=-2a,x2=![]() ,2a=
,2a=![]() ,
,
G(x1)-G(x2)=G(x1)-G(![]() )=
)=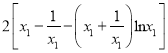
令H(x)=2[]![]() , H'(x)=2()
, H'(x)=2()![]() lnx=
lnx=![]()
当![]() 时,H/(x)<0, H(x)在
时,H/(x)<0, H(x)在![]() 上单调递减,H(x)的最小值为
上单调递减,H(x)的最小值为![]()
即G(x1)-G(x2) 的最小值为![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.得到下表:
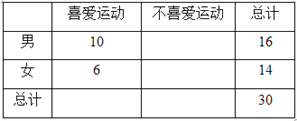
(1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.
(2)如果从喜欢运动的女志愿者中(其中恰有4人会外语)抽取2名,求抽出的志愿者中能胜任翻译工作的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: 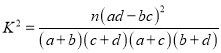
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①命题“![]() ,
, ![]() ”的否定是:“
”的否定是:“![]() ,
, ![]() ”;
”;
②若样本数据![]() 的平均值和方差分别为
的平均值和方差分别为![]() 和
和![]() 则数据
则数据![]() 的平均值和标准差分别为
的平均值和标准差分别为![]() ,
, ![]() ;
;
③两个事件不是互斥事件的必要不充分条件是两个事件不是对立事件;
④在![]() 列联表中,若比值
列联表中,若比值![]() 与
与![]() 相差越大,则两个分类变量有关系的可能性就越大.
相差越大,则两个分类变量有关系的可能性就越大.
⑤已知![]() 为两个平面,且
为两个平面,且![]() ,
, ![]() 为直线.则命题:“若
为直线.则命题:“若![]() ,则
,则![]() ”的逆命题和否命题均为假命题.
”的逆命题和否命题均为假命题.
⑥设定点![]() 、
、![]() ,动点
,动点![]() 满足条件
满足条件![]() 为正常数),则
为正常数),则![]() 的轨迹是椭圆.其中真命题的个数为( )
的轨迹是椭圆.其中真命题的个数为( )
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
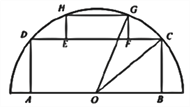
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池![]() 及其矩形附属设施
及其矩形附属设施![]() ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为
,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形的一边
,矩形的一边![]() 在直径上,点
在直径上,点![]() 在圆周上,
在圆周上, ![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,关于实数
,关于实数![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的不等式:
的不等式: ![]() ;
;
(2)是否存在实数![]() ,使得关于
,使得关于![]() 的函数
的函数![]() (
(![]() )的最小值为
)的最小值为![]() ?若存在,求实数
?若存在,求实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前![]() 项和为
项和为![]() ,数列{bn},{cn}满足
,数列{bn},{cn}满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切![]() ,有bn≤λ≤cn,求证:数列{an}是等差数列.
,有bn≤λ≤cn,求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某产品的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品![]() 千件
千件![]() 并全部销售完,每千件的销售收入为
并全部销售完,每千件的销售收入为![]() 万元,且
万元,且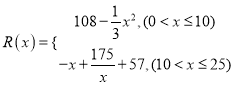 .
.
⑴ 写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
⑵ 当年产量为多少千件时,该公司在这一产品的生产中所获年利润最大?(注:年利润=年销售收入![]() 年总成本).
年总成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
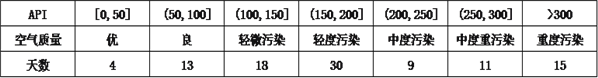
记某企业每天由空气污染造成的经济损失T(单位:元),空气质量指数API为![]() .在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为200元,当API为200时,造成的经济损失为400元);当API大于300时造成的经济损失为2000元.
.在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为200元,当API为200时,造成的经济损失为400元);当API大于300时造成的经济损失为2000元.
(1)试写出函数T(![]() )的表达式:
)的表达式:
(2)试估计在本年内随机抽取一天,该天经济损失大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关.
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
附: 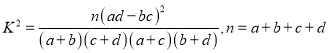
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com