
分析 建立空间直角坐标系,如图所示,M(0,0,0),A(-1,2,0),B(-1,0,0),C(1,0,0),D(1,2,0),E(0,0,$\sqrt{3}$),设点F(1,y,0),其中0≤y≤2;|AF|+|EF|=$\sqrt{4{+(y-2)}^{2}}$+$\sqrt{1{+y}^{2}+3}$=$\sqrt{{(y-2)}^{2}+4}$+$\sqrt{{y}^{2}+4}$,如图根据对称性,F为CD上的中点时,AF+EF最小,设四棱锥E-ABCD心为G(0,1,m)则GE=GC⇒m=$\frac{1}{\sqrt{3}}$,⇒四棱锥E-ABCD半径R2,同理三棱锥F-ABE的外接球半径r2,即可求四棱锥E-ABCD与三棱锥F-ABE的外接球的半径之比
解答 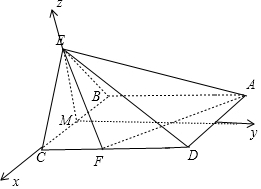 解:建立空间直角坐标系,如图所示,
解:建立空间直角坐标系,如图所示,
底面正方形ABCD的边长为2,△BCE为等边三角形,平面ABCD⊥平面BCE,
∴M(0,0,0),A(-1,2,0),B(-1,0,0),C(1,0,0),D(1,2,0),E(0,0,$\sqrt{3}$),
设点F(1,y,0),其中0≤y≤2;
|AF|+|EF|=$\sqrt{4{+(y-2)}^{2}}$+$\sqrt{1{+y}^{2}+3}$=$\sqrt{{(y-2)}^{2}+4}$+$\sqrt{{y}^{2}+4}$…①
①式表示在平面直角坐标系中点P(a,0)到点M(0,2),N(2,2)的距离和,如图根据对称性,可知a=1时,其距离和最小.
∴F为CD上的中点时,AF+EF最小,
设四棱锥E-ABCD心为G(0,1,m)
则GE=GC⇒m=$\frac{1}{\sqrt{3}}$,∴四棱锥E-ABCD半径R2=$\frac{7}{3}$
设三棱锥F-ABE的外接球球心H(x,y,z)
则HA=HB=HE=HF⇒x=-$\frac{1}{4}$,y=1,z=$\frac{5\sqrt{3}}{12}$.
三棱锥F-ABE的外接球半径r2=$\frac{25}{12}$,
四棱锥E-ABCD与三棱锥F-ABE的外接球的半径之比等于2$\sqrt{7}$:5
故答案为:2$\sqrt{7}$:5
点评 本题考查了空间几何体的外接球,涉及到了运用函数的知识处理动点问题,建立坐标系求球的球心,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5\sqrt{2}-12}{18}$ | B. | $\frac{-4\sqrt{2}-7}{9}$ | C. | $\frac{4-7\sqrt{2}}{9}$ | D. | $\frac{-4-7\sqrt{2}}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
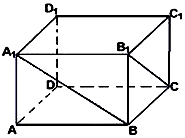 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
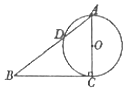 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD( )cm.
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD( )cm.| A. | 5 | B. | $\frac{16}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{17}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,4] | B. | [2,+∞) | C. | (2,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com