
 时,求二面角B-AC-P的大小.
时,求二面角B-AC-P的大小.
 (1)在平面β内过点C作CE⊥PQ于点E,由题知点E与点A不重合,连接EB.
(1)在平面β内过点C作CE⊥PQ于点E,由题知点E与点A不重合,连接EB. ∵BO⊥PQ,平面角α-PQ-β为直二面角,
∵BO⊥PQ,平面角α-PQ-β为直二面角, ,在Rt△OAB中,∠ABO=∠BAO=45°,所以BO=AO=
,在Rt△OAB中,∠ABO=∠BAO=45°,所以BO=AO= ,由CA=CB=kAB且
,由CA=CB=kAB且 得,AC=2,∴OC=1,则
得,AC=2,∴OC=1,则 .
.
 得
得

 ,由图可知,
,由图可知, .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
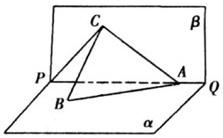 如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.
如图所示,PQ为平面α、β的交线,已知二面角α-PQ-β为直二面角,A∈PQ,B∈α,C∈β,CA=CB=kAB(k∈R*),∠BAP=45°.
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
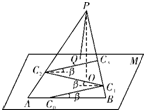 (2012•蓝山县模拟)某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=
(2012•蓝山县模拟)某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=| 2 |
| 5 |
| 1 |
| 4 |
| x2+100 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:黄冈重点作业·高二数学(下) 题型:047
如图所示,已知平面α∩β=MN,PQ α,KL
α,KL β,且PQ∥KL.设A∈PQ.AB⊥KL,AC⊥MN,垂足分别为B、C.
β,且PQ∥KL.设A∈PQ.AB⊥KL,AC⊥MN,垂足分别为B、C.

求证:MN⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC的中点,它的正(主)视图和侧(左)视图如图所示.
(1)证明:AD⊥平面PBC.
(2)求三棱锥D-ABC的体积.
(3)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com