
已知:如图,圆锥SO的轴截面是等腰直角三角形,其母线长为4a,A为底面圆周上一点,B是底面圆内一点,且OB⊥AB,C是SA的中点,D是O在SB上的射影.

(Ⅰ)求证:OD⊥平面SAB;
(Ⅱ)设平面SOA和平面SAB所成的二面角为θ(0<θ< ),问能否确定θ,使得三棱锥C—SOD的体积最大?若能,求出体积的最大值和对应的θ;若不能,请说明理由.
),问能否确定θ,使得三棱锥C—SOD的体积最大?若能,求出体积的最大值和对应的θ;若不能,请说明理由.
|
(1)证明 由SO垂直于⊙O所在平面,AB在⊙O内,可得AB⊥SO. ∵AB⊥SO,AB⊥OB,OB 而OD ∴OD⊥AB. 又OD⊥SB,SB ∴OD⊥平面SAB. (2)解 由圆锥SO的轴截面是等腰直角三角形,得OS=OA. 又C是SA的中点,∴OC⊥SA. 由OD⊥平面SAB,OC⊥SA,得DC⊥SA,∠OCD是平面SOA和平面SAB所成的二面角的平面角,则∠OCD=θ. 又∵OC⊥SA,DC⊥SA,OC ∴SA⊥平面COD. 由题意知:△COD是Rt△,且 故得: = 当且仅当OD=CD=
即存在θ= |


科目:高中数学 来源:2015届福建省高一下学期第一次月考数学试卷(解析版) 题型:解答题
如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求:

(1)设f(x)为绳子最短长度的平方,求f(x)表达式;
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市十校高三(下)第二次联考数学试卷(文科)(解析版) 题型:解答题
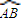 的中点,点P为母线SA的中点.若PQ与SO所成角为
的中点,点P为母线SA的中点.若PQ与SO所成角为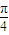 ,求此圆锥的全面积与体积.
,求此圆锥的全面积与体积.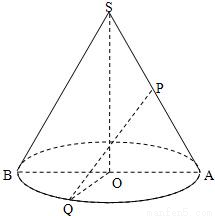
查看答案和解析>>
科目:高中数学 来源:2012年上海市普陀区高三年级第二次质量调研二模理科试卷(解析版) 题型:解答题
如图,已知圆锥体 的侧面积为
的侧面积为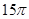 ,底面半径
,底面半径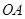 和
和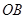 互相垂直,且
互相垂直,且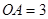 ,
, 是母线
是母线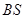 的中点.
的中点.

(1)求圆锥体的体积;
(2)异面直线 与
与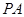 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
【解析】本试题主要考查了圆锥的体积和异面直线的所成的角的大小的求解。
第一问中,由题意, 得
得 ,故
,故
从而体积 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
解:(1)由题意, 得
得 ,
,
故 从而体积
从而体积 .
.
(2)如图2,取OB中点H,联结PH,AH.
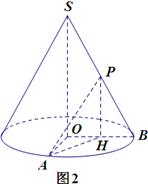
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com