
已知m= ,n=
,n= ,满足
,满足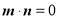 .
.
(1)将y表示为x的函数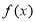 ,并求
,并求 的最小正周期;
的最小正周期;
(2)已知a,b,c分别为 ABC的三个内角A,B,C对应的边长,
ABC的三个内角A,B,C对应的边长, 的最大值是
的最大值是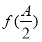 ,且a=2,求b+c的取值范围.
,且a=2,求b+c的取值范围.
科目:高中数学 来源:2013-2014学年山东省高三12月月考理科数学试卷(解析版) 题型:选择题
已知条件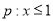 ,条件
,条件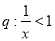 ,则
,则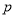 是
是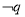 成立的 ( )
成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试理科数学试卷(解析版) 题型:选择题
“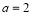 ”是“关于x的不等式
”是“关于x的不等式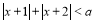 的解集非空”的( )
的解集非空”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试文科数学试卷(解析版) 题型:选择题
定义在R上的奇函数 满足
满足 ,且在
,且在 上是增函数,则有( )
上是增函数,则有( )
A.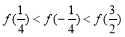 B.
B.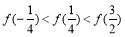
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试理科数学试卷(解析版) 题型:解答题
已知函数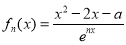 ,其中
,其中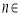 N*,a
N*,a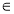 R,e是自然对数的底数.
R,e是自然对数的底数.
(1)求函数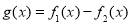 的零点;
的零点;
(2)若对任意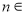 N*,
N*,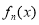 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知k,m N*,k<m,且函数
N*,k<m,且函数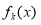 在R上是单调函数,探究函数
在R上是单调函数,探究函数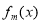 的单调性.
的单调性.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考文科数学试卷(解析版) 题型:选择题
对于三次函数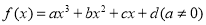 ,给出定义:设
,给出定义:设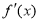 是函数
是函数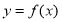 的导数,
的导数,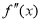 是
是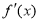 的导数,若方程
的导数,若方程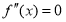 有实数解
有实数解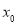 ,则称点
,则称点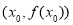 为函数
为函数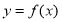 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数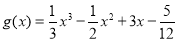 ,则
,则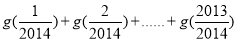 =( )
=( )
A. 2011 B. 2012 C. 2013 D. 2014
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试理科数学试卷(解析版) 题型:选择题
已知圆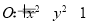 及以下三个函数:①
及以下三个函数:① ;②
;② ;③
;③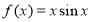 .其中图象能等分圆
.其中图象能等分圆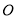 面积的函数个数为( )
面积的函数个数为( )
A.3 B.2 C.1 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com