
ЎѕМвДїЎїЎ¶»щґЎЅМУэїОіМёДёпёЩТЄ(КФРР)Ў·Ѕ«Ў°ѕЯУРБјєГµДРДАнЛШЦКЎ±БРИлРВїОіМµДЕаСшДї±кЈ®ОЄјУЗїРДАнЅЎїµЅМУэ№¤ЧчµДїЄХ№Ј¬І»¶ПМбёЯС§ЙъµДРДАнЛШЦКЈ¬ѕЕЅКРДіРЈёЯ¶юДкј¶їЄЙиБЛЎ¶РДАнЅЎїµЎ·СЎРЮїОЈ¬С§·ЦОЄ2·ЦЈ®С§РЈёщѕЭС§ЙъЖЅК±ЙПїО±нПЦёшіцЎ°єПёсЎ±УлЎ°І»єПёсЎ±БЅЦЦЖАјЫЈ¬»сµГЎ°єПёсЎ±ЖАјЫµДС§ЙъёшУи50·ЦµДЖЅК±·ЦЈ¬»сµГЎ°І»єПёсЎ±ЖАјЫµДС§ЙъёшУи30·ЦµДЖЅК±·ЦЈ¬БнНв»№Ѕ«ЅшРРТ»ґОІвСйЈ®С§ЙъЅ«ТФЎ°ЖЅК±·ЦЎБ40%+ІвСй·ЦЎБ80%Ў±ЧчОЄЎ°ЧоЦХµГ·ЦЎ±Ј¬Ў°ЧоЦХµГ·ЦЎ±І»ЙЩУЪ60·ЦХЯ»сµГС§·ЦЈ®
ёГРЈёЯ¶ю(1)°аСЎРЮЎ¶РДАнЅЎїµЎ·їОµДС§ЙъµДЖЅК±·Цј°ІвСй·ЦЅб№ыИзПВЈє
ІвСй·Ц | [30Ј¬40) | [40Ј¬50) | [50Ј¬60) | [60Ј¬70) | [70Ј¬80) | [80Ј¬90) | [90Ј¬100] |
ЖЅК±·Ц50·ЦИЛКэ | 0 | 1 | 1 | 3 | 4 | 4 | 2 |
ЖЅК±·Ц30·ЦИЛКэ | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
ЈЁ1Ј©ёщѕЭ±нЦРКэѕЭНкіЙИзПВ2ЎБ2БРБЄ±нЈ¬Іў·ЦОцКЗ·сУР95%µД°СОХИПОЄХвЩѧЙъЎ°ІвСй·ЦКЗ·сґпµЅ60·ЦЎ±УлЎ°ЖЅК±·ЦЎ±УР№ШБЄЈї
СЎРЮИЛКэ | ІвСй·Ц ґпµЅ60·Ц | ІвСй·Ц ОґґпµЅ60·Ц | єПјЖ |
ЖЅК±·Ц50·Ц | |||
ЖЅК±·Ц30·Ц | |||
єПјЖ |
ЈЁ2Ј©УГСщ±ѕ№АјЖЧЬМеЈ¬ИфґУЛщУРСЎРЮЎ¶РДАнЅЎїµЎ·їОµДС§ЙъЦРЛж»ъійИЎ5ИЛЈ¬Йи»сµГС§·ЦИЛКэОЄ![]() Ј¬Зу
Ј¬Зу![]() µДЖЪНыЈ®
µДЖЪНыЈ®
ёЅЈє![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]()
| 0Ј®1 | 0Ј®05 | 0Ј®025 | 0Ј®01 | 0Ј®005 | 0Ј®001 |
| 2Ј®706 | 3Ј®841 | 5Ј®024 | 6Ј®635 | 7Ј®879/p> | 10Ј®828 |
Ўѕґр°ёЎїЈЁ1Ј©УР95%µД°СОХИПОЄС§ЙъЎ°ІвСй·ЦКЗ·сґпµЅ60·ЦЎ±УлЎ°ЖЅК±·ЦЎ±УР№ШБЄЈ»ЈЁ2Ј©4
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭКэѕЭМо±нЈ¬И»єујЖЛг![]() Ј¬їЙµГЅб№ы.
Ј¬їЙµГЅб№ы.
ЈЁ2Ј©ёщѕЭјЖЛгЈ¬їЙµГОґ»сµГ·ЦКэµДИЛКэЈ¬И»єуїЙЦЄ»сµГ·ЦКэµДёЕВКЈ¬ТАѕЭ¶юПо·ЦІјКэС§ЖЪНыµДјЖЛг·Ѕ·ЁЈ¬їЙµГЅб№ы.
ЅвЈєЈЁ1Ј©ёщѕЭ±нЦРКэѕЭНіјЖЈ¬їЙµГ2x2БРБЄ±н
СЎРЮИЛКэ | ІвСй·Ц | єПјЖ | |
ґпµЅ60·Ц | ОґґпµЅ60·Ц | ||
ЖЅК±·Ц50·Ц | 13 | 2 | 15 |
ЖЅК±·Ц30·Ц | 2 | 3 | 5 |
єПјЖ | 15 | 5 | 20 |
![]()
![]() Ј¬
Ј¬
ЎаУР95%µД°СОХИПОЄС§ЙъЎ°ІвСй·ЦКЗ·сґпµЅ60·ЦЎ±УлЎ°ЖЅК±·ЦЎ±УР№ШБЄ
ЈЁ2Ј©·ЦОцС§ЙъµГ·ЦЈ¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
ЖЅК±·Ц50·ЦµДС§ЙъЦРІвСй·ЦЦ»РиґпµЅ50·ЦЈ¬
¶шЖЅК±·Ц30·ЦµДС§ЙъЦРІвСй·Ц±ШРлґпµЅ60·ЦЈ¬ІЕДЬ»сµГС§·Ц
ЖЅК±·Ц50·ЦµДС§ЙъІвСй·ЦОґґпµЅ50·ЦµДЦ»УР1ИЛЈ¬
ЖЅК±·Ц30·ЦµДС§ЙъІвСй·ЦОґґпµЅ60·ЦµДУР3ИЛ
ЎаґУХвЩѧЙъЦРЛж»ъійИЎ1ИЛЈ¬
ёГЙъ»сµГС§·ЦµДёЕВКОЄ![]()
![]() Ј¬
Ј¬![]() Ј®
Ј®


 РВМвРНИ«іМјмІвЖЪД©іеґМ100·ЦПµБРґр°ё
РВМвРНИ«іМјмІвЖЪД©іеґМ100·ЦПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪОеГжМе![]() ЦРЈ¬ІаГж
ЦРЈ¬ІаГж![]() КЗХэ·ЅРОЈ¬
КЗХэ·ЅРОЈ¬![]() КЗµИСьЦ±ЅЗИэЅЗРОЈ¬µг
КЗµИСьЦ±ЅЗИэЅЗРОЈ¬µг![]() КЗХэ·ЅРО
КЗХэ·ЅРО![]() ¶ФЅЗПЯµДЅ»µг
¶ФЅЗПЯµДЅ»µг![]() Ј¬
Ј¬![]() ЗТ
ЗТ![]() .
.

ЈЁ1Ј©Ц¤ГчЈє![]() ЖЅГж
ЖЅГж![]() Ј»
Ј»
ЈЁ2Ј©ИфІаГж![]() УлµЧГж
УлµЧГж![]() ґ№Ц±Ј¬ЗуОеГжМе
ґ№Ц±Ј¬ЗуОеГжМе![]() µДМе»э.
µДМе»э.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЦР№ъЎ°Т»ґшТ»В·Ў±ХЅВФ№№ЛјМбіцєу, ДіїЖјјЖуТµОЄЧҐЧЎЎ°Т»ґшТ»В·Ў±ґшАґµД»ъУц, ѕц¶ЁїЄ·ўЙъІъТ»їоґуРНµзЧУЙи±ё, ЙъІъХвЦЦЙи±ёµДДк№М¶ЁіЙ±ѕОЄ![]() НтФЄ, ГїЙъІъ
НтФЄ, ГїЙъІъ![]() МЁ,РиБнН¶ИліЙ±ѕ
МЁ,РиБнН¶ИліЙ±ѕ![]() (НтФЄ), µ±ДкІъБїІ»Чг
(НтФЄ), µ±ДкІъБїІ»Чг![]() МЁК±,
МЁК±,![]() (НтФЄ); µ±ДкІъБїІ»РЎУЪ
(НтФЄ); µ±ДкІъБїІ»РЎУЪ![]() МЁК±
МЁК±![]() (НтФЄ), ИфГїМЁЙи±ёКЫјЫОЄ
(НтФЄ), ИфГїМЁЙи±ёКЫјЫОЄ![]() НтФЄ, НЁ№эКРіЎ·ЦОц,ёГЖуТµЙъІъµДµзЧУЙи±ёДЬИ«ІїКЫНк.
НтФЄ, НЁ№эКРіЎ·ЦОц,ёГЖуТµЙъІъµДµзЧУЙи±ёДЬИ«ІїКЫНк.
ЈЁ1Ј©ЗуДкАыИу![]() (НтФЄ)№ШУЪДкІъБї
(НтФЄ)№ШУЪДкІъБї![]() ЈЁМЁЈ©µДєЇКэ№ШПµКЅЈ»
ЈЁМЁЈ©µДєЇКэ№ШПµКЅЈ»
ЈЁ2Ј©ДкІъБїОЄ¶аЙЩМЁК± ,ёГЖуТµФЪХвТ»µзЧУЙи±ёµДЙъІъЦРЛщ»сАыИуЧоґуЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїµгPОЄБЅЦ±ПЯl1Јє3x+4y©Ѓ2=0єНl2Јє2x+y+2=0µДЅ»µгЈ®
ЈЁ1Ј©Зу№эPµгЗТУлЦ±ПЯ3x©Ѓ2y+4=0ЖЅРРµДЦ±ПЯ·ЅіМЈ»
ЈЁ2Ј©Зу№эФµгЗТУлЦ±ПЯl1єНl2О§іЙµДИэЅЗРООЄЦ±ЅЗИэЅЗРОµДЦ±ПЯ·ЅіМЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЕЧОпПЯ![]() :
:![]() ЈЁ
ЈЁ![]() Ј©ЙПєбЧш±кОЄ4µДµгµЅЅ№µгµДѕаАлОЄ5Ј®
Ј©ЙПєбЧш±кОЄ4µДµгµЅЅ№µгµДѕаАлОЄ5Ј®
ЈЁ1Ј©ЗуЕЧОпПЯ![]() µД·ЅіМЈ»
µД·ЅіМЈ»
ЈЁ2Ј©ЙиЦ±ПЯ![]() УлЕЧОпПЯ
УлЕЧОпПЯ![]() Ѕ»УЪІ»Н¬БЅµг
Ѕ»УЪІ»Н¬БЅµг![]() Ј¬ИфВъЧг
Ј¬ИфВъЧг![]() Ј¬Ц¤ГчЦ±ПЯ
Ј¬Ц¤ГчЦ±ПЯ![]() єг№э¶ЁµгЈ¬ІўЗуіц¶Ёµг
єг№э¶ЁµгЈ¬ІўЗуіц¶Ёµг![]() µДЧш±кЈ®
µДЧш±кЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµ![]() ЦРЈ¬НЦФІ
ЦРЈ¬НЦФІ![]() µДІОКэ·ЅіМОЄ
µДІОКэ·ЅіМОЄ![]() ОЄІОКэ)Ј®ТФЧш±кФµг
ОЄІОКэ)Ј®ТФЧш±кФµг![]() ОЄј«µгЈ¬
ОЄј«µгЈ¬![]() ЦбµДХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµЈ¬Ц±ПЯ
ЦбµДХэ°лЦбОЄј«ЦбЅЁБўј«Чш±кПµЈ¬Ц±ПЯ![]() µДј«Чш±к·ЅіМОЄ
µДј«Чш±к·ЅіМОЄ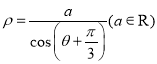 Ј¬Ц±ПЯ
Ј¬Ц±ПЯ![]() ѕ№эНЦФІ
ѕ№эНЦФІ![]() µДУТЅ№µг
µДУТЅ№µг![]() Ј®
Ј®
ЈЁ1Ј©ЗуКµКэ![]() µДЦµЈ»
µДЦµЈ»
ЈЁ2Ј©ЙиЦ±ПЯ![]() УлНЦФІ
УлНЦФІ![]() ПаЅ»УЪ
ПаЅ»УЪ![]() БЅµгЈ¬Зу
БЅµгЈ¬Зу![]() µДЦµЈ®
µДЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
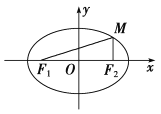
ЎѕМвДїЎїИзНјЛщКѕЈ¬![]() Ј¬
Ј¬![]() ·Ц±рОЄНЦФІµДЧуЈ¬УТЅ№µгЈ¬НЦФІЙПµг
·Ц±рОЄНЦФІµДЧуЈ¬УТЅ№µгЈ¬НЦФІЙПµг![]() µДєбЧш±кµИУЪУТЅ№µгµДєбЧш±кЈ¬ЖдЧЭЧш±кµИУЪ¶М°лЦбі¤µД
µДєбЧш±кµИУЪУТЅ№µгµДєбЧш±кЈ¬ЖдЧЭЧш±кµИУЪ¶М°лЦбі¤µД![]() Ј¬ФтНЦФІµДАлРДВКОЄЈЁ Ј©
Ј¬ФтНЦФІµДАлРДВКОЄЈЁ Ј©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄєЇКэ![]() .
.
ЈЁ1Ј©µ±![]() К±Ј¬МЦВЫ
К±Ј¬МЦВЫ![]() µДµјєЇКэ
µДµјєЇКэ![]() µДµҐµчРФЈ»
µДµҐµчРФЈ»
ЈЁ2Ј©µ±![]() К±Ј¬
К±Ј¬![]() Ј¬Зу
Ј¬Зу![]() µДИЎЦµ·¶О§.
µДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ТСЦЄНЦФІCЈє![]() µД¶МЦбі¤ОЄ2Ј¬ЗгР±ЅЗОЄ
µД¶МЦбі¤ОЄ2Ј¬ЗгР±ЅЗОЄ![]() µДЦ±ПЯlУлНЦФІCПаЅ»УЪAЈ¬BБЅµгЈ¬ПЯ¶ОABµДЦРµгОЄMЈ¬ЗТµгMУлЧш±кФµгOБ¬ПЯµДР±ВКОЄ
µДЦ±ПЯlУлНЦФІCПаЅ»УЪAЈ¬BБЅµгЈ¬ПЯ¶ОABµДЦРµгОЄMЈ¬ЗТµгMУлЧш±кФµгOБ¬ПЯµДР±ВКОЄ![]() .
.
ЈЁ1Ј©ЗуНЦФІCµД±кЧј·ЅіМЈ»
ЈЁ2Ј©Иф![]() Ј¬PКЗТФABОЄЦ±ѕ¶µДФІЙПµДИОТвТ»µгЈ¬ЗуЦ¤Јє
Ј¬PКЗТФABОЄЦ±ѕ¶µДФІЙПµДИОТвТ»µгЈ¬ЗуЦ¤Јє![]() .
.
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com