练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】端午节吃粽子是我国的传统习俗，设一盘中装有10个粽子，其中豆沙粽2个，肉粽3个，白粽5个，这三种粽子的外观完全相同，从中任意选取3个． （Ⅰ）求三种粽子各取到1个的概率；
    （Ⅱ）设X表示取到的豆沙粽个数，求X的分布列与数学期望．

    【答案】解：（Ⅰ）令A表示事件“三种粽子各取到1个”， 则由古典概型的概率公式有P（A）= = ．
    （Ⅱ）随机变量X的取值为：0，1，2，
    则P（X=0）= = ，P（X=1）= = ，P（X=2）= = ，

    X

    0

    1

    2

    P

    EX=0× +1× +2× =
    【解析】（Ⅰ）根据古典概型的概率公式进行计算即可；（Ⅱ）随机变量X的取值为：0，1，2，别求出对应的概率，即可求出分布列和期望．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校的学生文娱团队由理科组和文科组构成，具体数据如表所示：

    组别

    文科

    理科

    性别

    男生

    女生

    男生

    女生

    人数

    3

    1

    3

    2

    学校准备从该文娱团队中选出4人到某社区参加大型公益活动演出，每选出一名男生，给其所在的组记1分；每选出一名女生，给其所在的组记2分，要求被选出的4人中文科组和理科组的学生都有．
    （I）求理科组恰好得4分的概率；
    （II）记文科组的得分为X，求随机变量X的分布列和数学期望EX．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若函数在区间上存在零点，求实数的取值范围；

    （2）当时，若对任意的，总存在使成立，求实数的取值范围；

    （3）若的值域为区间，是否存在常数，使区间的长度为？若存在，求出的值，若不存在，请说明理由.（柱：区间的长度为）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设不等式x2+y2≤4确定的平面区域为U，|x|+|y|≤1确定的平面区域为V．
    （1）定义横、纵坐标为整数的点为“整点”，在区域U内任取3个整点，求这些整点中恰有2个整点在区域V的概率；
    （2）在区域U内任取3个点，记这3个点在区域V的个数为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（12分）

    （1）若函数在上为增函数，求实数的取值范围；

    （2）当时，求在上的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥P﹣ABC中．侧梭长均为4．底边AC=4．AB=2，BC=2 ，D．E分别为PC．BC的中点． 〔I）求证：平面PAC⊥平面ABC．
    （Ⅱ）求三棱锥P﹣ABC的体积；
    （Ⅲ）求二面角C﹣AD﹣E的余弦值．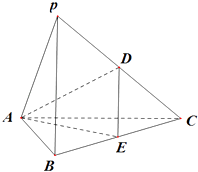

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某食品厂为了检查一条自动包装流水线的生产情况，随机抽取该流水线上的件产品作为样本，称出它们的重量（单位：克），重量的分组区间为，，…，，由此得到样本的频率分布方图，如图所示.

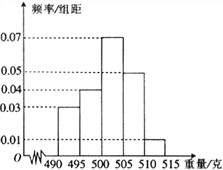
    （1）在上述抽取的件产品中任取件，设为取到重量超过克的产品件数，求的概率；

    （2）从上述件产品中任取件，设为取到重量超过克的产品件数，求的分布列与期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E： 的右焦点为F（3，0），过点F的直线交椭圆E于A、B两点．若AB的中点坐标为（1，﹣1），则E的方程为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地空气中出现污染，须喷洒一定量的去污剂进行处理.据测算，每喷洒1个单位的去污剂，空气中释放的浓度y（单位：毫克/立方米）随着时间x（单位：天）变化的函数关系式近似为，若多次喷洒，则某一时刻空气中的去污剂浓度为每次投放的去污剂在相应时刻所释放的浓度之和.由实验知，当空气中去污剂的浓度不低于4（毫克/立方米）时，它才能起到去污作用.

    （Ⅰ）若一次喷洒4个单位的去污剂，则去污时间可达几天？

    （Ⅱ）若第一次喷洒2个单位的去污剂，6天后再喷洒 个单位的去污剂，要使接下来的4天中能够持续有效去污，试求的最小值.

    查看答案和解析>>

    同步练习册答案