练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】函数y= 的定义域是（ ）
    A.（1，2]
    B.（1，2）
    C.（2，+∞）
    D.（﹣∞，2）

    【答案】B
    【解析】解：∵log2（x﹣1），∴x﹣1＞0，x＞1

    根据 ，得出x≤2，又在分母上不等于0，即x≠2

    ∴函数y= 的定义域是（1，2）

    故选B．

    【考点精析】根据题目的已知条件，利用函数的定义域及其求法和对数函数的定义域的相关知识可以得到问题的答案，需要掌握求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零；对数函数的定义域范围:（0，+∞）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列函数中，在其定义域既是奇函数又是减函数的是（ ）
    A.y=|x|
    B.y=﹣x3
    C.y=（ ）x
    D.y=

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，AB=AC=5，BB1=BC=6，D，E分别是AA1和B1C的中点
    （1）求证：DE∥平面ABC；
    （2）求三棱锥E﹣BCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（x﹣a）（x﹣b）（其中a＞b）的图象如图所示，则函数g（x）=b+logax的图象大致是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的三个顶点坐标分别为A（﹣1，1），B（7，﹣1），C（﹣2，5），AB边上的中线所在直线为l．
    （1）求直线l的方程；
    （2）若点A关于直线l的对称点为D，求△BCD的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一果农种植了1000棵果树，为估计其产量，从中随机选取20棵果树的产量（单位：kg）作为样本数据，得到如图所示的频率分布直方图．已知样本中产量在区间（45，50]上的果树棵数为8，

    （1）求频率分布直方图中a，b的值；
    （2）根据频率分布直方图，估计这20棵果树产量的中位数；
    （3）根据频率分布直方图，估计这1000棵果树的总产量．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】盒子中有5个大小形状完全相同的小球，其中黑色小球有3个，标号分别为1，2，3，白色小球有2个，标号分别为1，2．
    （1）若从盒中任取两个小球，求取出的小球颜色相同且标号之和小于或等于4的概率；
    （2）若盒子里再放入一个标号为4的红色小球，从中任取两个小球，求取出的两个小球颜色不同且标号之和大于3的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱锥S﹣ABC中，SA⊥底面ABC，AB⊥BC，DE垂直平分SC且分别交AC、SC于D、E，又SA=AB，SB=BC，

    （1）求证：BD⊥平面SAC；
    （2）求二面角E﹣BD﹣C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线y2=4 x的交点为椭圆 （a＞b＞0）的右焦点，且椭圆的长轴长为4，左右顶点分别为A，B，经过椭圆左焦点的直线l与椭圆交于C，D（异于A，B）两点．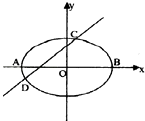

    （1）求椭圆标准方程；
    （2）求四边形ADBC的面积的最大值；
    （3）若M（x1 ， y1）N（x2 ， y2）是椭圆上的两动点，且满x1x2+2y1y2=0，动点P满足 （其中O为坐标原点），是否存在两定点F1 ， F2使得|PF1|+|PF2|为定值，若存在求出该定值，若不存在说明理由．

    查看答案和解析>>

    同步练习册答案