练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】随着经济的发展，人民的收入水平逐步提高，为了解北京市居民的收入水平，某报社随机调查了名居民的月收入，得到如下的频率分布直方图：

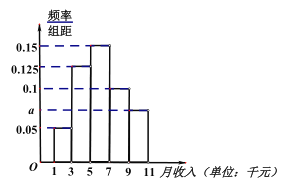
    （1）求的值及这名居民的平均月收入（同一组中的数据用该组区间的中点值作代表）

    （2）①通过大数据分析，北京人的月收入服从正态分布，其中，，求北京人收入落在的概率；

    ②将频率视为概率，若北京某公司一部门有人，记这人中月收入落在的人数为，求的数学期望.

    附：若，则

    【答案】(1);.(2)①，②.

    【解析】分析：（1）由已知得，则平均月收入；

    （2）①由题意结合正态分布的结论可知收入落在的概率为.

    ②由题意可得，则.

    详解：（1）由已知得：，

    解之得：，

    ；

    （2）①因为，所以

    所以.

    ②由频率分布直方图可知由频率分布直方图可知

    所以，

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知复数，是实数，是虚数单位．

    （1）求复数；

    （2）若复数所表示的点在第一象限，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P—ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：

    （1）PA∥平面MDB；

    （2）PD⊥BC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】央视传媒为了解央视举办的“朗读者”节目的收视时间情况，随机抽取了某市名观众进行调查，其中有名男观众和名女观众，将这名观众收视时间编成如图所示的茎叶图（单位：分钟），收视时间在分钟以上（包括分钟）的称为“朗读爱好者”，收视时间在分钟以下（不包括分钟）的称为“非朗读爱好者”.

    （1）若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取名，再从这名观众中任选名，求至少选到名“朗读爱好者”的概率；

    （2）若从收视时间在40分钟以上（包括40分钟）的所有观众中选出男、女观众各1名，求选出的这两名观众时间相差5分钟以上的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】今年4月的“西安奔驰女车主哭诉维权事件”引起了社会的广泛关注，某汽车4S店为了调研公司的售后服务态度，对5月份到店维修保养的100位客户进行了回访调查，每位客户用10分制对该店的售后服务进行打分．现将打分的情况分成以下几组：第一组[0，2），第二组[2，4），第三组[4，6），第四组[6，8），第五组[8，10]，得到频率分布直方图如图所示．已知第二组的频数为10．

    （1）求图中实数a，b的值；

    （2）求所打分值在[6，10]的客户人数；

    （3）总公司规定，若4S店的客户回访平均得分低于7分，则将勒令其停业整顿．试用频率分布直方图的组中值对总体平均数进行估计，判断该4S店是否需要停业整顿．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某中学甲、乙两班各随机抽取 名同学，测量他们的身高（单位： ），所得数据用茎叶图表示如下，由此可估计甲、乙两班同学的身高情况，则下列结论正确的是（ ）

    A. 甲班同学身高的方差较大 B. 甲班同学身高的平均值较大

    C. 甲班同学身高的中位数较大 D. 甲班同学身高在 以上的人数较多

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过抛物线 的焦点的直线与抛物线在第一象限的交点为，与抛物线准线的交点为 ，点在抛物线准线上的射影为，若 的面积为 .

    （ 1 ） 求抛物线的标准方程；

    （ 2 ） 过焦点的直线与抛物线交于两点，抛物线在点处的切线分别为，且与相交于点，与轴交于点，求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了让学生更多的了解“数学史”知识，某中学高二年级举办了一次“追寻先哲的足迹，倾听数学的声音”的数学史知识竞赛活动，共有800名学生参加了这次竞赛，为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，统计结果见下表.请你根据频率分布表解答下列问题：

    序号

    分组（分数）

    组中值

    频数（人数）

    频率

    1

    65

    ①

    0.12

    2

    75

    20

    ②

    3

    85

    ③

    0.24

    4

    95

    ④

    ⑤

    合计

    50

    1

    （1）填充频率分布表中的空格；

    （2）规定成绩不低于85分的同学能获奖，请估计在参加的800名学生中大概有多少名同学获奖？

    （3）在上述统计数据的分析中有一项计算见算法流程图，求输出的的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】羽毛球比赛中采用每球得分制，即每回合中胜方得1分，负方得0分，每回合由上回合的胜方发球．设在甲、乙的比赛中，每回合发球，发球方得1分的概率为0.6，各回合发球的胜负结果相互独立．若在一局比赛中，甲先发球．

    （1）求比赛进行3个回合后，甲与乙的比分为的概率；

    （2）表示3个回合后乙的得分，求的分布列与数学期望．

    查看答案和解析>>

    同步练习册答案