
【题目】已知函数![]()
 ,则方程
,则方程![]() (
(![]() 为正实数)的实数根最多有_____个
为正实数)的实数根最多有_____个
【答案】6
【解析】![]() .
.
![]() ,
,![]() ,
, ![]() 单调递增;
单调递增;
![]() ,
,![]() ,
, ![]() 单调递减;
单调递减;
![]() ,
,![]() ,
, ![]() 单调递增.
单调递增.
![]() .
.
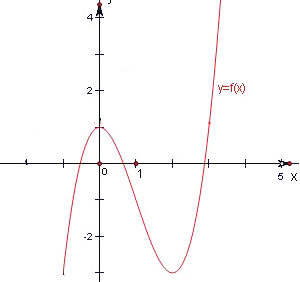
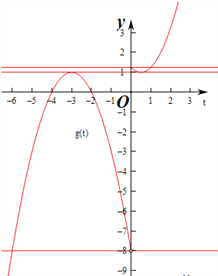
由g[f(x)]a=0(a>0)得g[f(x)]=a,(a>0)
设t=f(x),则g(t)=a,(a>0)
由y=g(t)的图象知,
①当0<a<1时,方程g(t)=a有两个根4<t1<3,或3<t2<2,
由t=f(x)的图象知,当4<t1<3时,t=f(x)有1个根,
当3<t2<2时,t=f(x)有3个根,
此时方程g[f(x)]a=0(a>0)有4个根,
②当a=1时,方程g(t)=a有两个根t1=3,或t2=![]() ,
,
由t=f(x)的图象知,当t1=3时,t=f(x)有2个根,
当t2=![]() 时,t=f(x)有3个根,
时,t=f(x)有3个根,
此时方程g[f(x)]a=0(a>0)有5个根,
③当![]() 时,方程g(t)=a有两个根0<t1<
时,方程g(t)=a有两个根0<t1<![]() ,或
,或![]() <t2<1,
<t2<1,
由t=f(x)的图象知,当0<t1<![]() 时,t=f(x)有3个根,
时,t=f(x)有3个根,
当![]() <t2<1时,t=f(x)有3个根,
<t2<1时,t=f(x)有3个根,
此时方程g[f(x)]a=0(a>0)有3+3=6个根,
④当a=![]() 时,方程g(t)=a有两个根t1=0,或t2=1,
时,方程g(t)=a有两个根t1=0,或t2=1,
由t=f(x)的图象知,当t1=0时,t=f(x)有3个根,
当t2=1时,t=f(x)有2个根,
此时方程g[f(x)]a=0(a>0)有3+2=5个根
⑤当a>![]() 时,方程g(t)=a有1个根t1>1,
时,方程g(t)=a有1个根t1>1,
由t=f(x)的图象知,当t1>1时,t=f(x)有1个根,
此时方程g[f(x)]a=0(a>0)有1个根,
综上方程g[f(x)]a=0(a>0)的实根最多有6个根,
答案为6.


科目:高中数学 来源: 题型:
【题目】中国在超级计算机方面发展迅速,跻身国际先进水平国家,预报天气的准确度也大大提高,天气预报说今后的三天中,每一天下雨的概率都是![]() ,我们可以通过随机模拟的方法估计概率.我们先产生
,我们可以通过随机模拟的方法估计概率.我们先产生![]() 组随机数
组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
在这组数中,用![]() 表示下雨,
表示下雨,![]() 表示不下雨,那么今后的三天中都下雨的概率近似为( )
表示不下雨,那么今后的三天中都下雨的概率近似为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算积分 .先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得积分
.先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得积分 的近似值为________.
的近似值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() 名学生参加学校组织的“数学竞赛集训队”选拔考试,现从中等可能抽出
名学生参加学校组织的“数学竞赛集训队”选拔考试,现从中等可能抽出![]() 名学生的成绩作为样本,制成如图频率分布表:
名学生的成绩作为样本,制成如图频率分布表:
分组 | 频数 | 频率 |
| 0.025 | |
| 0.050 | |
| 0.200 | |
| 12 | 0.300 |
| 0.275 | |
| 4 | |
| 0.00 | |
合计 |
| 1 |
(1)求![]() 的值,并根据题中信息估计总体平均数是多少?
的值,并根据题中信息估计总体平均数是多少?
(2)若成绩不低于![]() 分的同学能参加“数学竞赛集训队”,试估计该校大约多少名学生能参加“数学竞赛集训队”?
分的同学能参加“数学竞赛集训队”,试估计该校大约多少名学生能参加“数学竞赛集训队”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是临江公园内一个等腰三角形形状的小湖(假设湖岸是笔直的),其中两腰
是临江公园内一个等腰三角形形状的小湖(假设湖岸是笔直的),其中两腰![]() 米,
米,![]() .为了给市民营造良好的休闲环境,公园管理处决定在湖岸
.为了给市民营造良好的休闲环境,公园管理处决定在湖岸![]() ,
,![]() 上分别取点
上分别取点![]() ,
,![]() (异于线段端点),在湖上修建一条笔直的水上观光通道
(异于线段端点),在湖上修建一条笔直的水上观光通道![]() (宽度不计),使得三角形
(宽度不计),使得三角形![]() 和四边形
和四边形![]() 的周长相等.
的周长相等.

(1)若水上观光通道的端点![]() 为线段
为线段![]() 的三等分点(靠近点
的三等分点(靠近点![]() ),求此时水上观光通道
),求此时水上观光通道![]() 的长度;
的长度;
(2)当![]() 为多长时,观光通道
为多长时,观光通道![]() 的长度最短?并求出其最短长度.
的长度最短?并求出其最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置并证明;若不存在,说明理由.
的位置并证明;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com