
关于 的方程
的方程 ,给出下列四个题:
,给出下列四个题:
①存在实数 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数 ,使得方程恰有8个不同的实根。
,使得方程恰有8个不同的实根。
正确命题的序号为
①②③④
解析试题分析:关于x的方程(x2-1)2-|x2-1|+k=0可化为(x2-1)2-(x2-1)+k=0(x≥1或x≤-1)(1)
或(x2-1)2+(x2-1)+k=0(-1<x<1)(2)
当k=-2时,方程(1)的解为± ,方程(2)无解,原方程恰有2个不同的实根
,方程(2)无解,原方程恰有2个不同的实根
当k= 时,方程(1)有两个不同的实根±
时,方程(1)有两个不同的实根± ,方程(2)有两个不同的实根±
,方程(2)有两个不同的实根± ,
,
即原方程恰有4个不同的实根
当k=0时,方程(1)的解为-1,+1,± ,方程(2)的解为x=0,原方程恰有5个不同的实根当k=
,方程(2)的解为x=0,原方程恰有5个不同的实根当k= 时,方程(1)的解为±
时,方程(1)的解为± ,±
,± ,方程(2)的解为±
,方程(2)的解为±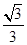 ,±
,± ,即原方程恰有8个不同的实根,∴四个命题都是真命题,故填写①②③④,
,即原方程恰有8个不同的实根,∴四个命题都是真命题,故填写①②③④,
考点:本题主要是考查了分段函数,以及函数与方程的思想,数形结合的思想,同时考查了分析问题的能力,属于中档题
点评:解决该试题的关键是将方程根的问题转化成函数图象的问题,画出函数图象,结合图象可得结论


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com