
【题目】已知函数f(x)=ax﹣sinx(a∈R).
(1)当![]() 时,f(x)
时,f(x)![]() 0恒成立,求正实数a的取值范围;
0恒成立,求正实数a的取值范围;
(2)当a≥1时,探索函数F(x)![]() f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
f(x)﹣cosx+a﹣1在(0,π)上的零点个数,并说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知分离参数后构造函数,转化为求解函数的最值或范围,结合导数可求;
(2)由已知结合导数分析函数的性质,然后结合函数的零点判定定理可求.
解:(1)因为![]() ,
,
所以![]() ,
,
令![]() ,
,![]() ,
,
再令m(x)![]() xcosx﹣sinx,m'(x)
xcosx﹣sinx,m'(x)![]() cosx﹣xsinx﹣cosx
cosx﹣xsinx﹣cosx![]() ﹣xsinx
﹣xsinx![]() 0,
0,
所以m(x)在(0,![]() )上单调递减,
)上单调递减,
所以m(x)![]() m(0)=0.
m(0)=0.
所以g'(x)![]() 0,则g(x)在(0,
0,则g(x)在(0,![]() )上单调递减,
)上单调递减,
所以g(x)![]() g(
g(![]() )
)![]() ,
,
所以a![]() ,
,
又a![]() 0,
0,
即正实数a的取值范围是(0,![]() ].
].
(2)F(x)![]() f(x)﹣cosx+a﹣1
f(x)﹣cosx+a﹣1![]() ax﹣sinx﹣cosx+a﹣1,
ax﹣sinx﹣cosx+a﹣1,
则![]() ,
,
因为x∈(0,π),
故![]() ,
,
又a≥1,
故F′(x)![]() 0对x∈(0,π)恒成立,
0对x∈(0,π)恒成立,
即F(x)在区间(0,π)单调递增;
又F(0)=a﹣2,F(π)=a(1+π)![]() 0,
0,
故当1≤a![]() 2时,F(0)=a﹣2
2时,F(0)=a﹣2![]() 0,此时F(x)在区间(0,π)内恰好有1个零点;
0,此时F(x)在区间(0,π)内恰好有1个零点;
当a≥2时,F(0)=a﹣2≥0,此时F(x)在区间(0,π)内没有零点.


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() ).若
).若![]() ,
,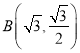 ,
,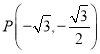 ,
,![]() 四点中有且仅有三点在椭面C上.
四点中有且仅有三点在椭面C上.
(1)求椭圆C的标准方程;
(2)设O为坐标原点,F为椭圆C的右焦点,过点F的直线l分别与椭圆C交于M,N两点,![]() ,求证:直线
,求证:直线![]() ,
,![]() 关于x轴对称.
关于x轴对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() 射线
射线![]() 交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
(1)求曲线C的直角坐标方程及直线l的参数方程;
(2)当直线l倾斜角α为何值时, |BP|·|BQ|取最小值, 并求出|BP|·|BQ|最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左、右焦点分别为F1、F2,过点F1作圆x2+y2=a2的切线交双曲线右支于点M,若tan∠F1MF2=2,又e为双曲线的离心率,则e2的值为( )
的左、右焦点分别为F1、F2,过点F1作圆x2+y2=a2的切线交双曲线右支于点M,若tan∠F1MF2=2,又e为双曲线的离心率,则e2的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2,△ADC沿AC折起,使得平面ADC⊥平面ABC,E为AB的中点,连接DE,DB(如图2).
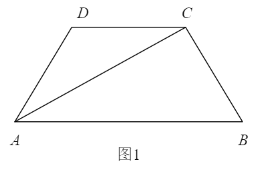
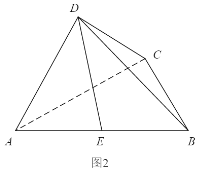
(1)求证:BC⊥AD
(2)求直线DE与平面BCD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,曲线
,曲线![]() 上任意一点到
上任意一点到![]() 的距离等于该点到直线
的距离等于该点到直线![]() 的距离.
的距离.
(Ⅰ)求![]() 及曲线
及曲线![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆只有一个交点
与椭圆只有一个交点![]() ,与曲线
,与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() ,问直线
,问直线![]() 是否存在?若存在,求直线
是否存在?若存在,求直线![]() 的斜率
的斜率![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春季,某出租汽车公同决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为11万元/辆和8万元/辆的A,B两款车型,根据以往这两种出租车车型的数据,得到两款出租车型使用寿命频数表如表:
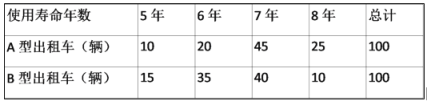
(1)填写如表,并判断是否有99%的把握认为出租车的使用寿命年数与汽车车有关?
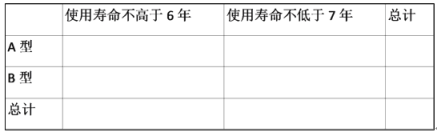
(2)以频率估计概率,从2020年生产的A和B的车型中各随机抽1车,以X表示这2车中使用寿命不低于7年的车数,求X的分布列和数学期望;
(3)根据公司要求,采购成本由出租公司负责,平均每辆出租每年上交公司6万元,其余维修和保险等费用自理,假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这100辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
参考公式: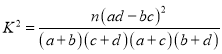 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
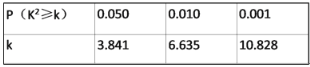
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com