
【题目】如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,PA⊥平面ABC,则四面体P-ABC的四个面中,直角三角形的个数有( )
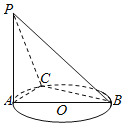
A. 4个B. 3个C. 2个D. 1个
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】某校在本校任选了一个班级,对全班50名学生进行了作业量的调查,根据调查结果统计后,得到如下的![]() 列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为
列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为![]() .
.
| 认为作业量大 | 认为作业量不大 | 合计 |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,能否有![]() 的把握认为“认为作业量大”与“性别”有关?
的把握认为“认为作业量大”与“性别”有关?
(Ⅲ)若视频率为概率,在全校随机抽取4人,其中“认为作业量大”的人数记为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn﹣1(x)的导函数,若输入函数f1(x)=sinx﹣cosx,则输出的函数fn(x)可化为( ) 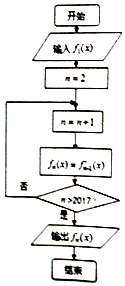
A.![]() sin(x+
sin(x+ ![]() )
)
B.![]() sin(x﹣
sin(x﹣ ![]() )??
)??
C.﹣ ![]() sin(x+
sin(x+ ![]() )
)
D.﹣ ![]() sin(x﹣
sin(x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
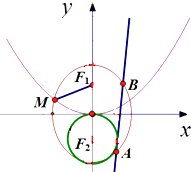
【题目】已知F1 , F2分别为椭圆C1: ![]() (a>b>0)的上下焦点,其F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|=
(a>b>0)的上下焦点,其F1是抛物线C2:x2=4y的焦点,点M是C1与C2在第二象限的交点,且|MF1|= ![]() .
. 
(1)试求椭圆C1的方程;
(2)与圆x2+(y+1)2=1相切的直线l:y=k(x+t)(t≠0)交椭圆于A,B两点,若椭圆上一点P满足 ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良101﹣150为轻度污染;151﹣200为中度污染;201~300为重度污染;>300为严重污染. 一环保人士记录去年某地某月10天的AQI的茎叶图如图.
(Ⅰ)利用该样本估计该地本月空气质量优良(AQI≤100)的天数;(按这个月总共30天)
(Ⅱ)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为ξ,求ξ的概率分布列和数学期望.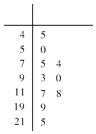
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:

(Ⅰ)根据茎叶图,计算甲班被抽取学生成绩的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若规定成绩不低于90分的等级为优秀,现从甲、乙两个班级所抽取成绩等级为优秀的学生中,随机抽取2人,求这两个人恰好都来自甲班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com