
【题目】设函数f(x)的定义域为D,若存在闭区间[a,b]D,使得函数f(x)满足:
①f(x)在[a,b]上是单调函数;
②f(x)在[a,b]上的值域是[2a,2b],则称区间[a,b]是函数f(x)的“和谐区间”.
下列结论错误的是( )
A.函数f(x)=x2(x≥0)存在“和谐区间”
B.函数f(x)=2x(x∈R)存在“和谐区间”
C.函数f(x)= ![]() (x>0)不存在“和谐区间”
(x>0)不存在“和谐区间”
D.函数f(x)=log2x(x>0)存在“和谐区间”
【答案】D
【解析】解:A中,当x≥0时,f(x)=x2在[0,2]上是单调增函数,且f(x)在[0,2]上的值域是[0,4],∴存在“和谐区间”,原命题正确;
B中,当x∈R时,f(x)=2x在[1,2]上是单调增函数,且f(x)在[1,2]上的值域是[2,4],∴存在“和谐区间”,原命题正确;
C中,f(x)= ![]() (x>0)是单调减函数,且f(x)在[1,2]上的值域是[
(x>0)是单调减函数,且f(x)在[1,2]上的值域是[ ![]() ,1],∴不存在“和谐区间”,原命题正确;
,1],∴不存在“和谐区间”,原命题正确;
D中,当x>0时,f(x)=log2x是单调增函数,假设存在[a,b]满足题意,则f(a)=2a,且f(b)=2b,即log2a=2a,且log2b=2b;
∴22a=a,且22b=b,即4a=a,且4b=b;这与函数的单调性矛盾,∴假设不成立,即函数不存在“和谐区间”,原命题不正确;
故选D.
【考点精析】认真审题,首先需要了解函数的值域(求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的).


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)=f′(1)ex﹣1﹣f(0)x+ ![]() x2;
x2;
(1)求f(x)的解析式及单调区间;
(2)若 ![]() ,求(a+1)b的最大值.
,求(a+1)b的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于函数f(x),若在定义域内存在实数x,满足f(﹣x)=﹣f(x),则称f(x)为“局部奇函数”.
(1)已知二次函数f(x)=ax2+2x﹣4a(a∈R),试判断f(x)是否为定义域R上的“局部奇函数”?若是,求出满足f(﹣x)=﹣f(x)的x的值;若不是,请说明理由;
(2)若f(x)=2x+m是定义在区间[﹣1,1]上的“局部奇函数”,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率P(A|B),P(B|A)分别是( )
A.![]() ,
, ![]()
B.![]() ,
, ![]()
C.![]() ,
, ![]()
D.![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
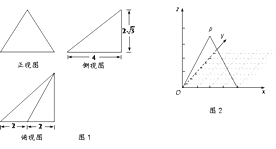
【题目】已知:三棱锥![]() 中,侧面
中,侧面![]() 垂直底面,
垂直底面, ![]() 是底面最长的边;图1是三棱锥
是底面最长的边;图1是三棱锥![]() 的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥
的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥![]() 的直观图的一部分,其中点
的直观图的一部分,其中点![]() 在
在![]() 平面内.
平面内.
(Ⅰ)请在图2中将三棱锥![]() 的直观图补充完整,并指出三棱锥
的直观图补充完整,并指出三棱锥![]() 的哪些面是直角三角形;
的哪些面是直角三角形;![]()
![]()
(Ⅱ)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值;
的值;
(Ⅲ)求点![]() 到面
到面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com