以点(-1,2)为圆心且与直线x+y-3=0相切的圆的方程是________.
(x+1)
2+(y-2)
2=2
分析:直线与圆相切时,圆心到直线的距离等于圆的半径,所以利用点到直线的距离公式求出圆心到已知直线的距离d,即为所求圆的半径r,然后由圆心和求出的r写出圆的标准方程即可.
解答:由所求的圆与直线x+y-3=0相切,
得到圆心(-1,2)到直线x+y-3=0的距离d=
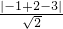
=

=r,
则所求圆的方程为:(x+1)
2+(y-2)
2=2.
故答案为:(x+1)
2+(y-2)
2=2
点评:此题考查了直线与圆的位置关系,以及圆的标准方程,直线与圆位置关系判别方法为:当d>r时,直线与圆相离;当d=r时,直线与圆相切;当0<d<r时,直线与圆相交(d为圆心到直线的距离,r为圆的半径),同时要求学生会根据圆心和半径写出圆的标准方程.

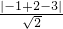 =
= =r,
=r,
