Question

如图，F₁，F₂是双曲线C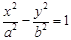：(a＞0，b＞0) 的左、右焦点，过F₁的直线与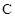的左、右两支分别交于A，B两点．若 | AB | : | BF₂ | : | AF₂ |＝3 : 4 : 5，则双 曲线的离心率为           .

 

Answer 1

【答案】

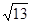
【解析】

试题分析：根据双曲线的定义可求得a=1，∠ABF₂=90°，再利用勾股定理可求得2c=|F₁F₂|，从而可求得双曲线的离心率．

解：∵|AB|：|BF₂|：|AF₂|=3：4：5，不妨令|AB|=3，|BF₂|=4，|AF₂|=5，∵|AB|²+|BF₂|2=|AF₂|2，∴∠ABF₂=90°，又由双曲线的定义得：|BF₁|-|BF₂|=2a，|AF₂|-|AF₁|=2a，∴|AF₁|+3-4=5-|AF₁|，∴|AF₁|=3．∴|BF₁|-|BF₂|=3+3-4=2a，

∴a=1．在Rt△BF₁F₂中，|F₁F₂|²=|BF₁|²+|BF₂|²=6²+4²=52，∵|F₁F₂|²=4c²，∴4c²=52，∴c=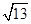，∴双曲线的离心率 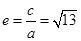，故答案为。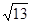

考点：双曲线的简单性质

点评：本题考查双曲线的简单性质，考查转化思想与运算能力，求得a与c的值是关键，属于中档题．