
【题目】设![]() .
.
(Ⅰ)若![]() 在其定义域内为单调递增函数,求实数
在其定义域内为单调递增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)设![]() ,且
,且![]() ,若在[1,e]上至少存在一点
,若在[1,e]上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)P≥1.(2)![]()
【解析】试题分析:(Ⅰ)首先求函数的导数, ![]() ,根据题意可得
,根据题意可得![]() ,当
,当![]() 恒成立,即求
恒成立,即求![]() 的最大值,
的最大值, 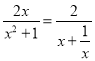 ,利用基本不等式求最大值;(Ⅱ)法一,原问题等价于
,利用基本不等式求最大值;(Ⅱ)法一,原问题等价于![]() ,求
,求![]() 的取值范围,法二,等价于
的取值范围,法二,等价于![]() 在
在![]() 上有解,即
上有解,即![]() ,求
,求![]() 的取值范围.
的取值范围.
试题解析:解:(I)由 f(x)=px﹣![]() ﹣2lnx,
﹣2lnx,
得![]() =
=![]() .
.
要使f(x)在其定义域(0,+∞)内为单调增函数,只需f′(x)≥0,
即px2﹣2x+p≥0在(0,+∞)内恒成立,
从而P≥1.
(II)解法1:g(x)=![]() 在[1,e]上是减函数,
在[1,e]上是减函数,
所以[g(x)]min=g(e)=2,[g(x)]max=g(1)=2e,即g(x)∈[2,2e].
当0<p<1时,由x∈[1,e],得x﹣![]() ,
,
故![]() ,不合题意.
,不合题意.
当P≥1时,由(I)知f(x)在[1,e]连续递增,f(1)=0<2,又g(x)在[1,e]上是减函数,
∴原命题等价于[f(x)]max>[g(x)]min=2,x∈[1,e],
由![]() ,解得
,解得![]()
综上,p的取值范围是(![]() ,+∞).
,+∞).
解法2:原命题等价于f(x)﹣g(x)>0在[1,e)上有解,
设F(x)=f(x)﹣g(x)=px﹣![]() ﹣2lnx﹣
﹣2lnx﹣![]() ,
,
∵![]()
=![]() ,
,
∴F(x)是增函数,
∴[F(x)]max=F(e)>0,解得![]()
∴p的取值范围是(![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】关于函数,给出下列命题:
①若函数f(x)是R上周期为3的偶函数,且满足f(1)=1,则f(2)-f(-4)=0;
②若函数f(x)满足f(x+1)f(x)=2 017,则f(x)是周期函数;
③若函数g(x)=![]() 是偶函数,则f(x)=x+1;
是偶函数,则f(x)=x+1;
④函数y=![]() 的定义域为
的定义域为![]() .
.
其中正确的命题是________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十八届五种全会公报指出:努力促进人口均衡发展,坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子的政策,提高生殖保健、妇幼保健、托儿等公共服务水平.为了解适龄公务员对放开生育二胎政策的态度,某部门随机调查了100位30到40岁的公务员,得到情况如下表:
男公务员 | 女公务员 | |
生二胎 | 40 | 20 |
不生二胎 | 20 | 20 |
(1)是否有95%以上的把握认为“生二胎与性别有关”,并说明理由;
(2)把以上频率当概率,若从社会上随机抽取3位30到40岁的男公务员,记其中生二胎的人数为![]() ,求随机变量
,求随机变量![]() 的分布列,数学期望.
的分布列,数学期望.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】倾斜角为![]() 的直线
的直线![]() 过点P(8,2),直线
过点P(8,2),直线![]() 和曲线C:
和曲线C: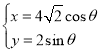 (
(![]() 为参数)交于不同的两点M1、M2.
为参数)交于不同的两点M1、M2.
(1)将曲线C的参数方程化为普通方程,并写出直线![]() 的参数方程;
的参数方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
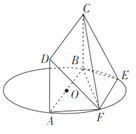
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 在圆
在圆![]() 上,
上, ![]() ,矩形
,矩形![]() 所在的平面与圆
所在的平面与圆![]() 所以的平面互相垂直,已知
所以的平面互相垂直,已知![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 的长为何值时,平面
的长为何值时,平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形, ![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长
的长![]() ,若不存在,请说明理由.
,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com