
【题目】已知{an}是等差数列,{bn}是各项均为正数的等比数列,且b1=a1=1,b3=a4,b1+b2+b3=a3+a4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
【答案】(1) ![]() ;(2)Tn=(n-1)·2n+1.
;(2)Tn=(n-1)·2n+1.
【解析】试题分析:
(1)设数列![]() 的公差为
的公差为![]() ,
, ![]() 的公比为
的公比为![]() ,运用等差数列和等比数列的通项公式,可得
,运用等差数列和等比数列的通项公式,可得![]() 的方程组,解方程可得公差和公比,即可得到所求通项公式;
的方程组,解方程可得公差和公比,即可得到所求通项公式;
(2)求得![]() ,运用乘公比错位相减法,结合等比数列的求和公式,化简整理即可得到所求的和.
,运用乘公比错位相减法,结合等比数列的求和公式,化简整理即可得到所求的和.
试题解析:
(1)设数列{an}的公差为d,{bn}的公比为q,
依题意得![]() 解得d=1,q=2.
解得d=1,q=2.
所以an=1+(n-1)×1=n,bn=1×2n-1=2n-1.
(2)由(1)知cn=anbn=n·2n-1,则
Tn=1·20+2·21+3·22+…+n·2n-1,①
2Tn=2·20+2·22+…+(n-1)·2n-1+n·2n,②
①-②得:-Tn=1+21+22+…+2n-1-n·2n
=![]() -n·2n=(1-n)·2n-1,
-n·2n=(1-n)·2n-1,
所以Tn=(n-1)·2n+1.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某项竞赛分为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是![]() 且各阶段通过与否相互独立.
且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为ξ,求ξ的分布列与均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·太原市模拟题)已知a,b,c分别是△ABC的内角A,B,C所对的边,a=2bcosB,b≠c.
(1)证明:A=2B;
(2)若a2+c2=b2+2acsinC,求A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为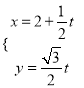 (t为参数),若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ-4cos θ=0.
(t为参数),若以该直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ-4cos θ=0.
(1)求直线l与曲线C的普通方程;
(2)已知直线l与曲线C交于A,B两点,设M(2,0),求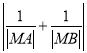 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
近年来,随着双十一、双十二等网络活动的风靡,各大网商都想出了一系列的降价方案,以此来提高自己的产品利润. 已知在2016年双十一某网商的活动中,某店家采取了两种优惠方案以供选择:
方案一:购物满400元以上的,超出400元的部分只需支出超出部分的x%;
方案二:购物满400元以上的,可以参加电子抽奖活动,即从1,2,3,4,5,6这6张卡牌中任取2张,将得到的数字相加,所得结果与享受优惠如下:
数字和 | [3,4] | [5,7] | [8,9] | [10,11] |
实际付款 | 原价 | 9折 | 8折 | 5折 |
(Ⅰ)若某顾客消费了800元,且选择方案二,求该顾客只需支付640元的概率;
(Ⅱ)若某顾客购物金额为500元,她选择了方案二后,得到的数字之和为6,此时她发现使用方案一、二最后支付的金额相同,求x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-aln x(a>0)的最小值是1.
(1)求a;
(2)若关于x的方程f2(x)ex-6mf(x)+9me-x=0在区间[1,+∞)有唯一的实根,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-ax+2lnx,a∈R.
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线垂直于直线y=x,求函数f(x)的单调区间;
(Ⅱ)若x>1时,f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com