
【题目】已知向量a=(cos α,sin α),b=(cos β,sin β),c=(-1,0).
(1) 求向量b+c的模的最大值;
(2) 若α=![]() ,且a⊥(b+c),求cos β的值.
,且a⊥(b+c),求cos β的值.
【答案】(1)2(2)见解析
【解析】试题分析(1)根据向量加法坐标表示以及向量模的坐标表示可得|b+c|2=2(1-cos β),再根据三角函数有界性可得模的最值(2)由向量垂直可得数量积为零,根据向量数量积坐标表示可得关于β的方程,解得β值 ,即得cos β的值.
试题解析:解:(1) b+c=(cos β-1,sin β),则|b+c|2=(cos β-1)2+sin2β=2(1-cos β).
∵ -1≤cos β≤1,
∴ 0≤|b+c|2≤4,即0≤|b+c|≤2.
当cos β=-1时,|b+c|取最大值2,
∴ 向量b+c的模的最大值为2.
(2) ∵ b+c=(cos β-1,sin β),
∴ a·(b+c)=cos αcos β-cos α+sin αsin β
=cos(α-β)-cos α.
∵ a⊥(b+c),
∴ a·(b+c)=0,即cos(α-β)=cos α.
又α=![]() ,∴ cos
,∴ cos![]() =cos
=cos![]() ,β-
,β-![]() =2kπ±
=2kπ±![]() (k∈Z),
(k∈Z),
∴ β=2kπ+![]() 或β=2kπ,k∈Z,
或β=2kπ,k∈Z,
∴ cos β=0或cos β=1.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
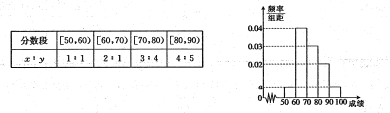
【题目】某校100名学生其中考试语文成绩的频率分布直方图所示,其中成绩分组区间是:
![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,
之比如下表所示,
求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足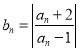 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
(B)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
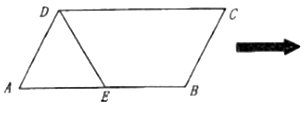
【题目】已知平行四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,且△
的中点,且△![]() 是等边三角形,沿
是等边三角形,沿![]() 把△
把△![]() 折起至
折起至![]() 的位置,使得
的位置,使得![]() .
.
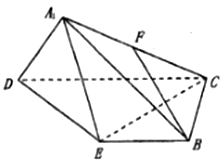
(1)![]() 是线段
是线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是 ( )
A. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内一定存在直线平行于平面
内一定存在直线平行于平面![]()
B. 如果平面![]() 不垂直平面
不垂直平面![]() ,那么平面
,那么平面![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面![]()
C. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,那么
,那么![]()
D. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com