
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨,生产每吨乙产品要用A原料1吨,B原料3吨。销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是___________万元
【答案】获得最大利润为27万元.
【解析】试题分析:设生产甲产品![]() 吨,生产乙产品
吨,生产乙产品![]() 吨,则依题意可列出x,y的不等式组,然后画出不等式组表示的平面区域,利用目标函数的几何意义求出最值即可.
吨,则依题意可列出x,y的不等式组,然后画出不等式组表示的平面区域,利用目标函数的几何意义求出最值即可.
试题解析: 设生产甲产品![]() 吨,生产乙产品
吨,生产乙产品![]() 吨,则有关系:
吨,则有关系:
A原料 | B原料 | |
甲产品 | 3 | 2 |
乙产品 |
| 3 |
则有: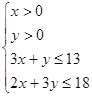 ,目标函数
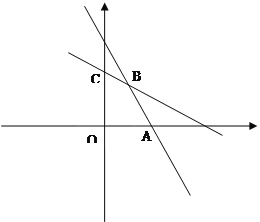
,目标函数![]() ,不等式组表示的平面区域为四边形OABC(不包含线段OC、OA)及其内部, 如图所示,且B(3,4),而目标函数
,不等式组表示的平面区域为四边形OABC(不包含线段OC、OA)及其内部, 如图所示,且B(3,4),而目标函数![]() 可看作是直线
可看作是直线![]() 在y轴上的截距,显然在过点B时截距最大,且此时z最大,最大值为
在y轴上的截距,显然在过点B时截距最大,且此时z最大,最大值为![]() 万元.
万元.
故当![]() =3,
=3,![]() =4时可获得最大利润为27万元,
=4时可获得最大利润为27万元,
答:生产甲产品3吨,乙产品4吨,可使该企业获得最大利润27万元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
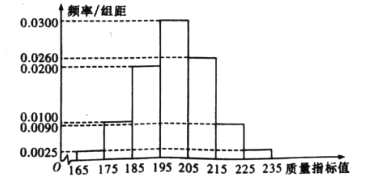
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足an=2Sn﹣1(n∈N*) (Ⅰ)求证:数列{an}为等比数列;
(Ⅱ)若bn=(2n+1)an , 求{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
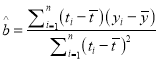 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图. 
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)估计用电量落在[220,300)中的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com