
(2005
全国Ⅱ,22)已知a≥0,函数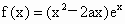 .
.
(1)
当x为何值时,f(x)取得最小值?证明你的结论;(2)
设f(x)在[-1,1]上是单调函数,求a的取值范围.科目:高中数学 来源: 题型:044
(2005
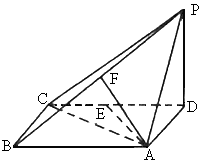
全国Ⅱ,20)如下图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点.(1)
求证:EF⊥平面PAB;(2)
设AB=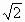 BC,求AC与平面AEF所成的角的大小.
BC,求AC与平面AEF所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2005
全国Ⅲ,18)如下图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.(1)
证明:AB⊥平面VAD;(2)
求面VAD与面VDB所成的二面角的大小.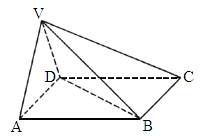
查看答案和解析>>
科目:高中数学 来源: 题型:
【练40】(1)(2005全国卷Ⅲ)△ABC中,内角A,B,C的对边分别是a,b,c,已知a,b,c成等比数列,且cosB=![]() 。(1)求cotA+cotC的值;(2)设
。(1)求cotA+cotC的值;(2)设![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com