

| �ŷ� | ���ŷ� | �ϼ� | |
| ���� | |||
| �� | |||
| �ϼ� | 50 |
| P��K2��k2�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 0.46 | 0.71 | 1.32 | 2.07 | 2.71 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ������ƽ�����Ķ���ֱ����������Ů����ƽ���ɼ����ɣ�
����2��2�������������������k��ֵ���Ƚϼ��ɣ�
����ͨ���ֲ�����ķ�����ȡ����$\frac{30}{50}$��5=3���ˣ�����Ϊa��b��c��Ů��$\frac{20}{50}$��5=2����Ϊ��1��2��������������ĸ��ʼ��ɣ�
��� �⣺������������Ů����ƽ���ɼ��ֱ���$\overline{{x}_{1}}$��$\overline{{x}_{2}}$��
��${\overline{x}}_{1}$=45��0.1+55��0.1+65��0.2+75��0.3+85��0.2+95��0.1=72��
${\overline{x}}_{2}$=$\frac{1}{20}$[40+50��2+60��2+70��4+80��7+90��4+��4+3+5+19+32+4��]=76.35��
���������ͼʾ����2��2������������������ͼʾ��
| �ŷ� | ���ŷ� | �ܼ� | |
| ���� | 9 | 21 | 30 |
| �� | 11 | 9 | 20 |
| �ܼ� | 20 | 30 | 50 |
���� ���⿼���˶����Լ������⣬���鿼��ֲ�����Լ����ʵļ��㣬��һ���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15�� | B�� | 30�� | C�� | 45�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{3}$ | B�� | $\frac{5}{3}$ | C�� | $\frac{5}{4}$ | D�� | $\frac{7}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{-�ޣ�-\frac{1}{e}}��$ | B�� | ��-�ޣ�-e�� | C�� | ��e��+�ޣ� | D�� | $��{\frac{1}{e}��+��}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{11}{3}$ | B�� | 5 | C�� | -8 | D�� | -11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
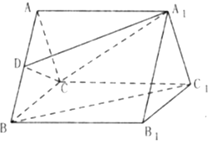 ��ͼ����������ABC-A1B1C1�У����ⴹֱ���棬���ⳤ��Ϊ2��DΪAB���е㣮
��ͼ����������ABC-A1B1C1�У����ⴹֱ���棬���ⳤ��Ϊ2��DΪAB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com