
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据(单位:万元):
之间有如下的对应数据(单位:万元):
![]()
(1)求![]() 关于
关于![]() 的线性回归直线方程;
的线性回归直线方程;
(2)据此估计广告费用为10万元时销售收入![]() 的值.
的值.
(附:对于线性回归方程![]() ,其中
,其中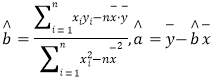 )
)
参考公式: 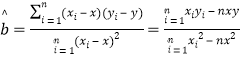
【答案】(1)![]() (2)82.5
(2)82.5
【解析】试题分析:(1)根据所给的数据先做出横坐标和纵坐标的平均数,利用最小乘法写出线性回归方程系数的表达式,把样本中心点代入求出![]() 的值,得到线性回归方程;(2)根据所给的变量
的值,得到线性回归方程;(2)根据所给的变量![]() 的值,把值代入线性回归方程,得到对应的
的值,把值代入线性回归方程,得到对应的![]() 的值,这里的
的值,这里的![]() 的值是一个预报值.
的值是一个预报值.
试题解析:(1) ![]() ,
,
![]()
![]() ,
,![]() ,
,
所以 ![]() ,
,![]()
所以回归直线方程为![]() ..
..
(2)![]() 时,预报
时,预报![]() 的值为
的值为![]() 万元
万元
【方法点晴】本题主要考查回归分析和线性回归方程,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是内角A,B,C的对边,且(a+c)2=b2+3ac.
(Ⅰ)求角B的大小;
(Ⅱ)若b=2,且sinB+sin(C﹣A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m≠0,向量 ![]() =(m,3m),向量
=(m,3m),向量 ![]() =(m+1,6),集合A={x|(x﹣m2)(x+m﹣2)=0}.
=(m+1,6),集合A={x|(x﹣m2)(x+m﹣2)=0}.
(1)判断“ ![]() ∥
∥ ![]() ”是“|
”是“| ![]() |=
|= ![]() ”的什么条件
”的什么条件
(2)设命题p:若 ![]() ⊥
⊥ ![]() ,则m=﹣19,命题q:若集合A的子集个数为2,则m=1,判断p∨q,p∧q,¬q的真假,并说明理由.
,则m=﹣19,命题q:若集合A的子集个数为2,则m=1,判断p∨q,p∧q,¬q的真假,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC为一个等腰三角形形状的空地,腰CA的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2 . 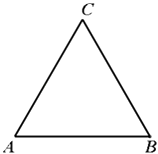
(1)若小路一端E为AC的中点,求此时小路的长度;
(2)求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出的v值为( ) 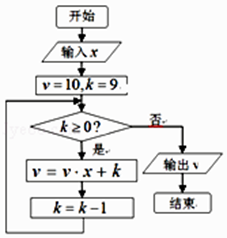
A.9×210﹣2
B.9×210+2
C.9×211+2
D.9×211﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(|x+1|+|x﹣2|﹣m).
(1)当m=7时,求函数f(x)的定义域;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现采取随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示集中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数: 7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击四次至少击中三次的概率为: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1与双曲线C2有相同的左右焦点F1、F2 , P为椭圆C1与双曲线C2在第一象限内的一个公共点,设椭圆C1与双曲线C2的离心率为e1 , e2 , 且 ![]() =
= ![]() ,若∠F1PF2=
,若∠F1PF2= ![]() ,则双曲线C2的渐近线方程为( )
,则双曲线C2的渐近线方程为( )
A.x±y=0
B.x± ![]() y=0
y=0
C.x± ![]() y=0
y=0
D.x±2y=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com