【答案】
分析:(I)连结A
1B,设A
1B交AB
1于E,连结DE.根据三角形的中位线定理,证出DE∥A
1C,结合线面垂直的判定定理,即可得到
A
1C∥平面AB
1D;
(II)根据等边△ABC的中线,证出AD⊥BC,结合面面垂直的性质定理,证出AD⊥平面B
1BCC
1,从而得到AD⊥BC
1.矩形B
1C
1CB中利用Rt△B
1BD∽Rt△BCC
1,证出BC
1⊥B
1D.最后根据线面垂直判定定理,即可证出BC
1⊥平面AB
1D.
解答:解:(Ⅰ)连结A
1B,设A
1B交AB
1于E,连结DE.
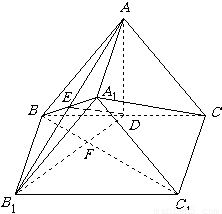
∵△A
1BC中,点D是BC的中点,点E是A
1B的中点,
∴DE∥A
1C. …(3分)
∵A
1C?平面AB
1D,DE?平面AB
1D,
∴A
1C∥平面AB
1D. …(6分)
(Ⅱ)∵△ABC是正三角形,点D是BC的中点,
∴AD⊥BC.
∵平面ABC⊥平面B
1BCC
1,平面ABC∩平面B
1BCC
1=BC,AD?平面ABC,
∴AD⊥平面B
1BCC
1.
∵BC
1?平面B
1BCC
1,∴AD⊥BC
1.…(9分)
∵点D是BC中点,
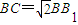
,∴
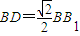
.
由此可得:

,
∴Rt△B
1BD∽Rt△BCC
1,可得∠BDB
1=∠BC
1C.
∴∠FBD+∠BDF=∠C
1BC+∠BC
1C=90°
∴BC
1⊥B
1D,…(13分)
∵B
1D∩AD=D,B
1D、AD?平面AB
1D,
∴BC
1⊥平面AB
1D. …(15分)
点评:本题给出底面为矩形且一个侧面为垂直于底面的正三角形的四棱锥,求证线面平行和线面垂直.着重考查了空间线面平行的判定定理、面面垂直的性质定理和线面垂直的判定与性质等知识,属于中档题.

 .设B1D∩BC1=F.
.设B1D∩BC1=F.

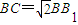 ,∴
,∴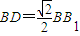 .
. ,
,

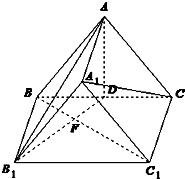 (2008•江苏二模)正三棱柱A1B1C1-ABC中,点D是BC的中点,BC=
(2008•江苏二模)正三棱柱A1B1C1-ABC中,点D是BC的中点,BC=