函数f(x)=a2x+2ax-1(a>0,且a≠1)
(1)若a=2,求y=f(x)的值域
(2)若y=f(x)在区间[-1,1]上有最大值14.求a的值;
(3)在(2)的前题下,若a>1,作出f(x)=a|x-1|的草图,并通过图象求出函数f(x)的单调区间.
【答案】
分析:(1)当a=2时,f(x)=2
2x+2×2
x-1=(2
x+1)
2-2,利用二次函数的性质即可求解
(2)y=a
2x+2a
x-1=(a
x+1)
2-2对于底数a分类讨论得到函数的最值和单调性.
(3)结合指数函数的图象及函数的图象的平移即可
解答:解:(1)当a=2时,f(x)=2
2x+2×2
x-1=(2
x+1)
2-2
∵2
x>0,设t=2
x,则y=(t+1)
2-2在(0,+∞)上单调递增
故y>-1,∴y=f(x)的值域为(-1,+∞)….(5分)
(2)y=a
2x+2a
x-1=(a
x+1)
2-2….(6分)
①当a>1时,又-1≤x≤1,可知
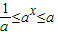
,设a
x=t,
则y=(t+1)
2-2在[

]上单调递增
∴

,解得a=3或a=-5,故a=3…(8分)
②当0<a<1时,又-1≤x≤1,可知

,设a
x=t,
则y=(t+1)
2-2在[

]上单调递增
∴

,解得

,故

…(10分)
综上可知a的值为3或

…(11分)
(3)y=3
|x-1|的图象,

…..(13分)
函数的单调递增区间为(1,+∞),单调递减区间为(-∞,1)…(14分)
点评:本题主要考查了指数函数的值域的求解,二次函数在闭区间上的最值的求解及函数的图象的平移及对称变换,体现了数形结合及分类讨论思想的应用

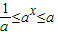 ,设ax=t,
,设ax=t, ]上单调递增
]上单调递增 ,解得a=3或a=-5,故a=3…(8分)
,解得a=3或a=-5,故a=3…(8分) ,设ax=t,
,设ax=t, ]上单调递增
]上单调递增 ,解得
,解得 ,故
,故 …(10分)
…(10分) …(11分)
…(11分) …..(13分)
…..(13分)

 名校课堂系列答案
名校课堂系列答案