
【题目】若函数f(x)=x2﹣ex﹣ax在R上存在单调递增区间,则实数a的取值范围是 .
【答案】(﹣∞,2ln2﹣2)
【解析】解:∵函数f(x)=x2﹣ex﹣ax,
∴f′(x)=2x﹣ex﹣a,
∵函数f(x)=x2﹣ex﹣ax在R上存在单调递增区间,
∴f′(x)=2x﹣ex﹣a>0,
即a<2x﹣ex有解,
令g′(x)=2﹣ex ,
g′(x)=2﹣ex=0,x=ln2,
g′(x)=2﹣ex>0,x<ln2,
g′(x)=2﹣ex<0,x>ln2
∴当x=ln2时,g(x)max=2ln2﹣2,
∴a<2ln2﹣2即可.
所以答案是:(﹣∞,2ln2﹣2)
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).


科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
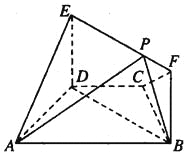
(1)求证:AD⊥平面BFED;
(2)已知点P在线段EF上,![]() =2.求三棱锥E-APD的体积.
=2.求三棱锥E-APD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知曲线C1:y=![]() (x>0)及曲线C2:y=
(x>0)及曲线C2:y=![]() (x>0).C1上的点Pn的横坐标为an,
(x>0).C1上的点Pn的横坐标为an,![]() 过C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再过点Qn作直线平行于y轴,交曲线C1于点Pn+1.
过C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再过点Qn作直线平行于y轴,交曲线C1于点Pn+1.
试求an+1与an之间的关系,并证明a2n-1<![]() <a2n(n∈N+).
<a2n(n∈N+).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 ![]() (其中θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0.
(其中θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0.
(1)分别写出曲线C1与曲线C2的普通方程;
(2)若曲线C1与曲线C2交于A,B两点,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年,首都北京经历了59年来雾霾天气最多的一个月.经气象局统计,北京市从1月1日至1月30日的30天里有26天出现雾霾天气,《环境空气质量指数(AQI)技术规定(试行)》将空气质量指数分为六级,其中,中度污染(四级)指数为151~200;重度污染(五级)指数为201~300;严重污染(六级)指数大于300.下面表1是某观测点记录的4天里AQI指数M与当天的空气水平可见度y(千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数的统计结果.
表1
AQI指数M | 900 | 700 | 300 | 100 |
空气可见度y/千米 | 0.5 | 3.5 | 6.5 | 9.5 |
表2
AQI指数 | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设变量x=![]() ,根据表1的数据,求出y关于x的线性回归方程;
,根据表1的数据,求出y关于x的线性回归方程;
(2)根据表2估计这30天AQI指数的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知Q2=![]() 称为x,y的二维平方平均数,A2=
称为x,y的二维平方平均数,A2=![]() 称为x,y的二维算术平均数,G2=
称为x,y的二维算术平均数,G2=![]() 称为x,y的二维几何平均数,H2=
称为x,y的二维几何平均数,H2=![]() 称为x,y的二维调和平均数,其中x,y均为正数.
称为x,y的二维调和平均数,其中x,y均为正数.
(1)试判断G2与H2的大小,并证明你的猜想.
(2)令M=A2﹣G2,N=G2﹣H2,试判断M与N的大小,并证明你的猜想.
(3)令M=A2﹣G2,N=G2﹣H2,P=Q2﹣A2,试判断M、N、P三者之间的大小关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com