
【题目】已知椭圆E: ![]() 的离心率为
的离心率为![]() ,过左焦点作x轴的垂线交椭圆于A、B两点,且|AB|=1.
,过左焦点作x轴的垂线交椭圆于A、B两点,且|AB|=1.
(1)求椭圆E的方程;
(2)设P、Q是椭圆E上两点,P在第一象限,Q在第二象限,且OP⊥OQ,其中O是坐标原点.
当P、Q运动时,是否存在定圆O,使得直线PQ都与定圆O相切?若存在,请求出圆O的方程;若不存在,请说明理由.
【答案】(1)![]() +y2=1. (2)存在定圆O:
+y2=1. (2)存在定圆O: ![]() 使得直线PQ与定圆O相切.
使得直线PQ与定圆O相切.
【解析】试题分析:(1)利用![]() ,解得
,解得![]() ,由此求得椭圆方程.(2)设出直线的方程,联立直线的方程和椭圆方程,写出韦达定理,将
,由此求得椭圆方程.(2)设出直线的方程,联立直线的方程和椭圆方程,写出韦达定理,将![]() 转化为两个向量的数量积为零,可求得
转化为两个向量的数量积为零,可求得![]() 的一个关系式.由于直线和圆相切,利用圆心到直线的距离等于半径可求得半径为定值.
的一个关系式.由于直线和圆相切,利用圆心到直线的距离等于半径可求得半径为定值.
试题解析:
(1)因为e=![]() ,所以
,所以![]() =
=![]() ,通径长
,通径长![]() ,
, ![]() 解得
解得![]() ,
, ![]() ,故椭圆的方程为
,故椭圆的方程为![]() +y2=1. (2)设PQ方程为y=kx+m 代入椭圆方程
+y2=1. (2)设PQ方程为y=kx+m 代入椭圆方程![]() +y2=1.
+y2=1.
化简得![]() 设P(x1,y1) Q(x2,y2)
设P(x1,y1) Q(x2,y2)
由韦达定理得![]()
![]()
![]()
![]()
![]()
![]()
![]() 化简得
化简得![]()
假设存在定圆![]() 与直线PQ相切,半径为r,则圆心到直线的距离d=r
与直线PQ相切,半径为r,则圆心到直线的距离d=r
为定值
所以当P,Q运动时, 存在定圆![]() :
: ![]() 使得直线PQ与定圆
使得直线PQ与定圆![]() 相切.
相切.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() N*
N*
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知![]() (
(![]() N*),记
N*),记![]()
![]() (
(![]() 且
且![]() ),是否存在这样的常数
),是否存在这样的常数![]() ,使得数列
,使得数列![]() 是常数列,若存在,求出
是常数列,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)若数列![]() ,对于任意的正整数
,对于任意的正整数![]() ,均有
,均有
 成立,求证:数列
成立,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
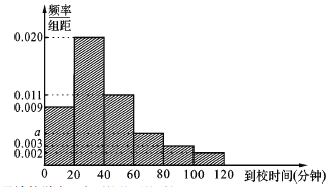
(1)求![]() 的值及该校学生从家到校的平均时间;
的值及该校学生从家到校的平均时间;
(2)若该校因学生寝室不足,只能容纳全校![]() 的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60), ...,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩在[40,50)和[90,100]的学生中任选两人,求他们在同一分数段的概率.
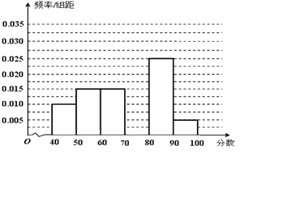
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深![]() (米)是随着一天的时间
(米)是随着一天的时间![]() 呈周期性变化,某天各时刻
呈周期性变化,某天各时刻![]() 的水深数据的近似值如下表:
的水深数据的近似值如下表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 2.4 | 1.5 | 0.6 | 1.4 | 2.4 | 1.6 | 0.6 | 1.5 |
(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从
①![]() , ②
, ②![]() ,③
,③![]()
![]() 中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ) 中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是偶函数,对于x∈R都有f(x+6)=f(x)+f(3)成立.当x1,x2∈[0,3],且x1≠x2时,都有![]() >0,给出下列命题:
>0,给出下列命题:
① f(3)=0;
② 直线x=-6是函数y=f(x)的图象的一条对称轴;
③ 函数y=f(x)在[-9,-6]上为单调递减函数;
④ 函数y=f(x)在[-9,9]上有4个零点.
其中正确的命题是____________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(A)设函数![]() ,
, ![]() .
.
(1)证明:函数![]() 在
在![]() 上为增函数;
上为增函数;
(2)若方程![]() 有且只有两个不同的实数根,求实数
有且只有两个不同的实数根,求实数![]() 的值.
的值.
(B)已知函数![]() .
.
(1)求函数![]() 的最小值;
的最小值;
(2)若存在唯一实数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com