
【题目】近年来,手机已经成为人们日常生活中不可缺少的产品,手机的功能也日趋完善,已延伸到了各个领域,如拍照,聊天,阅读,缴费,购物,理财,娱乐,办公等等,手机的价格差距也很大,为分析人们购买手机的消费情况,现对某小区随机抽取了200人进行手机价格的调查,统计如下:
年龄 价格 | 5000元及以上 | 3000元﹣4999元 | 1000元﹣2999元 | 1000元以下 |
45岁及以下 | 12 | 28 | 66 | 4 |
45岁以上 | 3 | 17 | 46 | 24 |
(Ⅰ)完成关于人们使用手机的价格和年龄的2×2列联表,再判断能否在犯错误的概率不超过0.025的前提下,认为人们使用手机的价格和年龄有关?
(Ⅱ)从样本中手机价格在5000元及以上的人群中选择3人调查其收入状况,设3人中年龄在45岁及以下的人数为随机变量X,求随机变量X的分布列及数学期望.
附K2= ![]()
P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】解:(Ⅰ)关于人们使用手机的价格和年龄的2×2列联表如下:
3000元及以上 | 3000元以下 | 总计 | |
45岁及以下 | 40 | 70 | 110 |
45岁以上 | 20 | 70 | 90 |
总计 | 60 | 140 | 200 |
根据2×2列联中的数据可得K2= ![]() ≈4.714<5.024,
≈4.714<5.024,
∴在犯错概率不超过0.025的前提下,不能认为“人们使用手机的价格和年龄有关”;
(Ⅱ)由表可知手机价格在5000元及其以上的人数为15,
从中选择3人,年龄在45岁及以下的人数X的可能取值为:0,1,2,3,
P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
P(X=3)= ![]() =
= ![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴E(X)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =
= ![]()
【解析】(1)分别计算出年龄在45岁上下的人数,求出K2的值,判断在犯错概率不超过0.025的前提下认为“人们使用手机的价格和年龄有关”;(2)先确定X的取值,分别求其概率,求出分布列和数学期望.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣1﹣a(x+lnx),a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线为x轴,求a的值:
(2)在(1)的条件下,求f(x)的单调区间;
(3)若x>0,f(x)≥f(m)恒成立,且f(m)≥0,求证:f(m)≥2(m2﹣m3).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2+lnx,a∈R. (Ⅰ)若曲线y=f(x)与直线y=3x+b在x=1处相切,求实数a,b的值;
ax2+lnx,a∈R. (Ⅰ)若曲线y=f(x)与直线y=3x+b在x=1处相切,求实数a,b的值;
(Ⅱ)求函数y=f(x)的单调区间;
(Ⅲ)若a=0时,函数h(x)=f(x)+bx有两个不同的零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程ρ=2cosθ,直线l的参数方程是 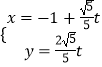 (t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(t为参数). (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设直线l与y轴的交点是M,N是曲线C上一动点,求|MN|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线的中心在坐标原点O,M、N分别为双曲线虚轴的上、下端点,A是双曲线的右顶点,F是双曲线的右焦点,直线AM与FN相交于点P,若∠APF是锐角,则此双曲线的离心率的取值范围是( ) 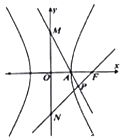
A.( ![]() ,+∞)
,+∞)
B.(1+ ![]() ,+∞)
,+∞)
C.(0, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣ ![]() |﹣|2x+1|. (Ⅰ)求f(x)的值域;
|﹣|2x+1|. (Ⅰ)求f(x)的值域;
(Ⅱ)若f(x)的最大值时a,已知x,y,z均为正实数,且x+y+z=a,求证: ![]() +
+ ![]() +
+ ![]() ≥1.
≥1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 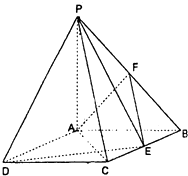
(1)证明:无论点E在BC边的何处,都有PE⊥AF;
(2)当BE等于何值时,PA与平面PDE所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,与函数y=﹣e|x|的奇偶性相同,且在(﹣∞,0)上单调性也相同的是( )
A.![]()
B.y=ln|x|
C.y=x3﹣3
D.y=﹣x2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com