
【题目】某人上午7时乘船出发,以匀速![]() 海里/小时
海里/小时![]() 从
从![]() 港前往相距50海里的
港前往相距50海里的![]() 港,然后乘汽车以匀速
港,然后乘汽车以匀速![]() 千米/小时(
千米/小时(![]() )自
)自![]() 港前往相距
港前往相距![]() 千米的
千米的![]() 市,计划当天下午4到9时到达
市,计划当天下午4到9时到达![]() 市.设乘船和汽车的所要的时间分别为
市.设乘船和汽车的所要的时间分别为![]() 、
、![]() 小时,如果所需要的经费
小时,如果所需要的经费![]() (单位:元)
(单位:元)

(1)试用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() ;
;
(2)要使得所需经费![]() 最少,求
最少,求![]() 和
和![]() 的值,并求出此时的费用.
的值,并求出此时的费用.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)分析题意,先用![]() 表示
表示![]() ,先用
,先用![]() 表示
表示![]() ,代入
,代入![]() ,化简即可;(2)求出
,化简即可;(2)求出![]() 满足的约束条件,由约束条件画出可行域,要求走得最经济,即求可行域中的最优解,将目标函数看成是一条直线,分析目标函数
满足的约束条件,由约束条件画出可行域,要求走得最经济,即求可行域中的最优解,将目标函数看成是一条直线,分析目标函数![]() 与直线截距的关系,进而求出最优.
与直线截距的关系,进而求出最优.
试题解析:(1) ![]() ,得
,得![]()
![]() ,得
,得![]()
![]()
所以![]() (其中
(其中![]() )
)
(2) ![]()
其中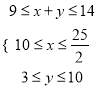 ,
,
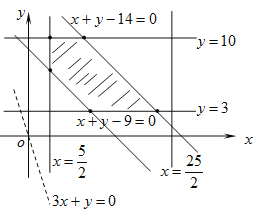
令目标函数![]() ,可行域的端点分别为
,可行域的端点分别为![]()
则当![]() 时,
时, ![]()
所以![]() (元),此时
(元),此时![]()
答:当![]() 时,所需要的费用最少,为
时,所需要的费用最少,为![]() 元.
元.
【方法点晴】本题主要考查线性规划的应用及求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.


科目:高中数学 来源: 题型:
【题目】空气质量主要受污染物排放量及大气扩散等因素的影响,某市环保监测站2014年10月连续10天(从左到右对应1号至10号)采集该市某地平均风速及空气中氧化物的日均浓度数据,制成散点图如图所示.
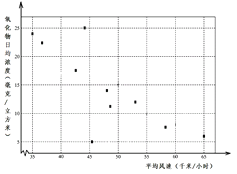
(Ⅰ)同学甲从这10天中随机抽取连续5天的一组数据,计算回归直线方程.试求连续5天的一组数据中恰好同时包含氧化物日均浓度最大与最小值的概率;
(Ⅱ)现有30名学生,每人任取5天数据,对应计算出30个不同的回归直线方程.已知30组数据中有包含氧化物日均浓度最值的有14组.现采用这30个回归方程对某一天平均风速下的氧化物日均浓度进行预测,若预测值与实测值差的绝对值小于2,则称之为“拟合效果好”,否则为“拟合效果不好”.根据以上信息完成下列2×2联表,并分析是否有95%以上的把握说拟合效果与选取数据是否包含氧化物日均浓度最值有关.
预测效果好 | 拟合效果不好 | 合计 | |
数据有包含最值 | 5 | ||
数据无包含最值 | 4 | ||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
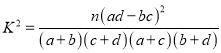 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点(![]() ,-2).
,-2).
(1)求φ的值;
(2)若f(![]() )=
)=![]() ,-
,-![]() <α<0,求sin(2α-
<α<0,求sin(2α-![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
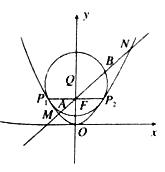
【题目】如图,抛物线![]() 的准线为
的准线为![]() ,取过焦点
,取过焦点![]() 且平行于
且平行于![]() 轴的直线与抛物线交于不同的两点
轴的直线与抛物线交于不同的两点![]() ,过
,过![]() 作圆心为
作圆心为![]() 的圆,使抛物线上其余点均在圆外,且
的圆,使抛物线上其余点均在圆外,且![]() .
.
(Ⅰ)求抛物线![]() 和圆
和圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与抛物线
与抛物线![]() 和圆
和圆![]() 依次交于
依次交于![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点,求证: 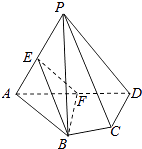
(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥ABCD﹣PGFE中,底面ABCD是直角梯形,侧棱垂直于底面,AB∥DC,∠ABC=45°,DC=1,AB=2,PA=1.
(Ⅰ)求PD与BC所成角的大小;
(Ⅱ)求证:BC⊥平面PAC;
(Ⅲ)求二面角A﹣PC﹣D的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com