
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 是
是![]() 上一点,直线
上一点,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() =
=
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
先根据题意写出直线的方程,再将直线的方程与抛物线y2=2x的方程组成方程组,消去y得到关于x的二次方程,最后利用根与系数的关系结合抛物线的定义即可求线段AB的长.
解:抛物线C:y2=2x的焦点为F(![]() ,0),准线为l:x=﹣
,0),准线为l:x=﹣![]() ,设M(x1,y1),N(x2,y2),M,N到准线的距离分别为dM,dN,
,设M(x1,y1),N(x2,y2),M,N到准线的距离分别为dM,dN,
由抛物线的定义可知|MF|=dM=x1+![]() ,|NF|=dN=x2+
,|NF|=dN=x2+![]() ,于是|MN|=|MF|+|NF|=x1+x2+1.
,于是|MN|=|MF|+|NF|=x1+x2+1.
∵![]() ,则
,则![]() ,易知:直线MN的斜率为±
,易知:直线MN的斜率为±![]() ,
,
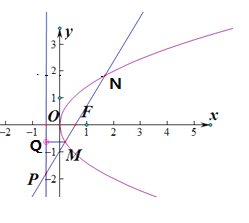
∵F(![]() ,0),
,0),
∴直线PF的方程为y=±![]() (x﹣
(x﹣![]() ),
),
将y=±![]() (x﹣
(x﹣![]() ),代入方程y2=2x,得3(x﹣
),代入方程y2=2x,得3(x﹣![]() )2=2x,化简得12x2﹣20x+3=0,
)2=2x,化简得12x2﹣20x+3=0,
∴x1+x2![]() ,于是|MN|=x1+x2+1
,于是|MN|=x1+x2+1![]() 1
1![]()
故选:B.


科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() .
.
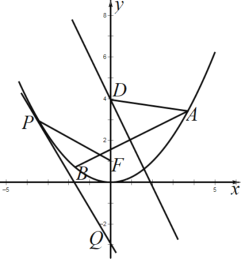
![]() 若点
若点![]() 为抛物线上异于原点的任一点,过点
为抛物线上异于原点的任一点,过点![]() 作抛物线的切线交
作抛物线的切线交![]() 轴于点
轴于点![]() ,证明:
,证明:![]() .
.
![]()
![]() ,
,![]() 是抛物线上两点,线段
是抛物线上两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() (
(![]() 不与
不与![]() 轴平行),且
轴平行),且![]() .过
.过![]() 轴上一点
轴上一点![]() 作直线
作直线![]() 轴,且
轴,且![]() 被以
被以![]() 为直径的圆截得的弦长为定值,求
为直径的圆截得的弦长为定值,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着时代的发展和社会的进步,“农村淘宝”发展十分迅速,促进“农产品进城”和“消费品下乡”.“农产品进城”很好地解决了农产品与市场的对接问题,使农民收入逐步提高,生活水平得到改善,农村从事网店经营的人收入逐步提高.西凤脐橙是四川省南充市的特产,因果实呈椭圆形、色泽橙红、果面光滑、无核、果肉脆嫩化渣、汁多味浓,深受人们的喜爱.为此小王开网店销售西凤脐橙,每月月初购进西凤脐橙,每售出1吨西凤脐橙获利润800元,未售出的西凤脐橙,每1吨亏损500元.经市场调研,根据以往的销售统计,得到一个月内西凤脐橙市场的需求量的频率分布直方图如图所示.小王为下一个月购进了100吨西凤脐橙,以x(单位:吨)表示下一个月内市场的需求量,y(单位:元)表示下一个月内经销西凤脐橙的销售利润.
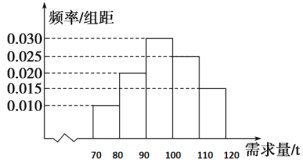
(1)将y表示为x的函数;
(2)根据频率分布直方图估计小王的网店下一个月销售利润y不少于67000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率,(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求小王的网店下一个月销售利润y的分布列和数学期望.
的频率),求小王的网店下一个月销售利润y的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 的底面
的底面![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]()
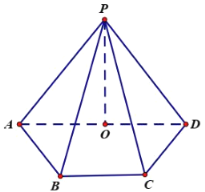
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() ?若存在指出点
?若存在指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数x都有
,且对任意的实数x都有![]() (e是自然对数的底数),且
(e是自然对数的底数),且![]() ,若关于x的不等式
,若关于x的不等式![]() 的解集中恰有两个整数,则实数m的取值范围是( )
的解集中恰有两个整数,则实数m的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 为椭圆上一动点(异于左右顶点),
为椭圆上一动点(异于左右顶点),![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点(如图1).将
的中点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 的中点(如图2).
的中点(如图2).
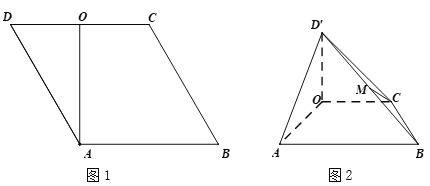
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)当四棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com