
分析 (1)x≥0时,得到f(x)=$x-\frac{1}{1+{x}^{2}}+1$,根据增函数的定义,设任意的x1>x2≥0,然后作差,通分,提取公因式x1-x2,证明f(x1)>f(x2),从而得出f(x)在[0,+∞)上单调递增;
(2)容易判断f(x)为偶函数,从而由f(x)>f(2x-1)便可得到f(|x|)>f(|2x-1|),由(1)便可得出|x|>|2x-1|,对该不等式两边平方便可得出该不等式的解集,即得出原不等式的解集.
解答 解:(1)证明:x≥0时,$f(x)=x-\frac{1}{1+{x}^{2}}+1$;
设x1>x2≥0,则:
$f({x}_{1})-f({x}_{2})={x}_{1}-\frac{1}{1+{{x}_{1}}^{2}}-{x}_{2}+\frac{1}{1+{{x}_{2}}^{2}}$=$({x}_{1}-{x}_{2})[1+\frac{{x}_{1}+{x}_{2}}{(1+{{x}_{1}}^{2})(1+{{x}_{2}}^{2})}]$;
∵x1>x2≥0;
∴x1-x2>0,x1+x2>0,$1+\frac{{x}_{1}+{x}_{2}}{(1+{x}_{1})^{2}(1+{{x}_{2}}^{2})}>0$;
∴f(x1)>f(x2);
∴f(x)在[0,+∞)上单调递增;
(2)f(x)定义域为R,且f(-x)=f(x);
∴f(x)为偶函数,且在[0,+∞)上单调递增;
∴由f(x)>f(2x-1)得:f(|x|)>f(|2x-1|);
∴|x|>|2x-1|;
解得$\frac{1}{3}<x<1$;
∴原不等式的解集为($\frac{1}{3},1$).
点评 考查含绝对值函数的处理方法:去绝对值号,增函数的定义,以及根据增函数的定义证明一个函数为增函数的方法和过程,作差的方法比较f(x1),f(x2),作差后是分式的一般要通分,一般要提取公因式x1-x2,偶函数的定义,根据函数的单调性解不等式,以及绝对值不等式的解法.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| A. | 7m/s | B. | 6m/s | C. | 2m/s | D. | 1m/s |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
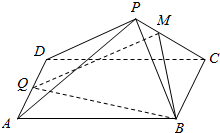 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,Q为AD的中点,点M在线段PC上且PM=tPC(t>0),试确定实数t的值,使得PA∥平面MQB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | 2$\sqrt{2}$-2 | D. | 2$\sqrt{2}$-$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=-1 | B. | m=-2 | C. | m=-1或2 | D. | m=l或m=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com