【题目】设
，
是两个平面，
，
是两条直线，下列命题错误的是（ ）
A.如果
，
，那么
.
B.如果
，
，那么
.
C.如果，，
，那么
.
D.如果内有两条相交直线与平行，那么.
优等生题库系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，
是椭圆上一动点（与左、右顶点不重合）已知
的内切圆半径的最大值为
，椭圆的离心率为
.
（1）求椭圆C的方程；
（2）过的直线
交椭圆
于
两点，过
作
轴的垂线交椭圆与另一点
（不与重合）.设
的外心为
，求证
为定值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】十九大指出中国的电动汽车革命早已展开，通过以新能源汽车替代汽/柴油车，中国正在大力实施一项将重塑全球汽车行业的计划．2018年某企业计划引进新能源汽车生产设备，通过市场分析，全年需投入固定成本2500万元，每生产x（百辆），需另投入成本
万元，且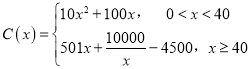
．由市场调研知，每辆车售价5万元，且全年内生产的车辆当年能全部销售完．
（1）求出2018年的利润L（x）（万元）关于年产量x（百辆）的函数关系式；（利润=销售额-成本）
（2）2018年产量为多少百辆时，企业所获利润最大?并求出最大利润．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数
与仰卧起坐
个数
之间的关系如下：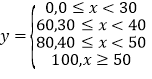
；测试规则：每位队员最多进行三组测试，每组限时1分钟，当一组测完，测试成绩达到60分或以上时，就以此组测试成绩作为该队员的成绩，无需再进行后续的测试，最多进行三组；根据以往的训练统计，队员“喵儿”在一分钟内限时测试的频率分布直方图如下：
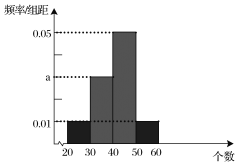
（1）计算
值；
（2）以此样本的频率作为概率，求
①在本次达标测试中，“喵儿”得分等于
的概率；
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）若函数
与
有相同的极值点（极值点是指函数取极值时对应的自变量的值），求
的值；
（2）记
.
①若在区间
（
为自然对数底数）上至少存在一点
，使得
成立，求的取值范围；
②若函数
图象存在两条经过原点的切线，求的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商家统计了去年
，
两种产品的月销售额（单位：万元），绘制了月销售额的雷达图，图中
点表示产品2月份销售额约为20万元，
点表示产品9月份销售额约为25万元.
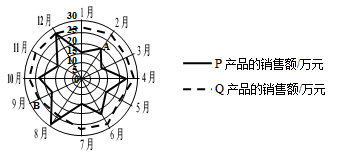
根据图中信息，下面统计结论错误的是（ ）
A.产品的销售额极差较大B.产品销售额的中位数较大
C.产品的销售额平均值较大D.产品的销售额波动较小
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左顶点为A1，右焦点为F2，过点F2作垂直于x轴的直线交该椭圆于M、N两点，直线A1M的斜率为
．
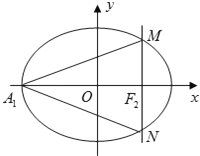
（Ⅰ）求椭圆的离心率；
（Ⅱ）若△A1MN的外接圆在M处的切线与椭圆相交所得弦长为
，求椭圆方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某港口某天0时至24时的水深
（米）随时间
（时）变化曲线近似满足如下函数模型
（
）.若该港口在该天0时至24时内，有且只有3个时刻水深为3米，则该港口该天水最深的时刻不可能为（ ）
A.16时B.17时C.18时D.19时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
