
【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
上年度出险次数 | 0 | 1 | 2 | 3 |
|
保费(元) |
|
|
|
|
|
随机调查了该险种的200名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 |
|
频数 | 140 | 40 | 12 | 6 | 2 |
该保险公司这种保险的赔付规定如下表:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
| 0 |
将所抽样本的频率视为概率。
(1)求本年度—续保人保费的平均值的估计值;
(2)求本年度—续保人所获赔付金额的平均值的估计值;
(3)据统计今年有100万投保人进行续保,若该公司此险种的纯收益不少于900万元,求![]() 的最小值(纯收益=总入保额-总赔付额)。
的最小值(纯收益=总入保额-总赔付额)。
【答案】(1) ![]() (2)
(2) ![]() (3) 100元
(3) 100元
【解析】
(1)先计算出每个保费对应的概率,然后按照平均值的计算公式计算出平均值的估计值.(2)先计算出每个赔偿金额对应的概率,然后按照平均值的计算公式,计算出平均值的估计值.(3)根据(1)(2)计算的结果计算出纯收益为![]() ,使
,使![]() 求得
求得![]() 的最小值.
的最小值.
解:(1)由题意可得
保费(元) |
|
|
|
|
|
概率 | 0.7 | 0.2 | 0.06 | 0.03 | 0.01 |
∴本年度一续保人保费的平均值的估计值为
![]() ;
;
(2)由题意可得
赔偿金额(元) | 0 |
|
|
|
|
概率 | 0.7 | 0.2 | 0.06 | 0.03 | 0.01 |
∴本年度一续保人所获赔付金额的平均值的估计值
![]() ;
;
(3)由(1),(2)得该公司此险种的总收益为![]() ,
,
∴![]() ,∴
,∴![]() ,∴基本保费
,∴基本保费![]() 的最小值为100元。
的最小值为100元。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】袋子中有大小、形状完全相同的四个小球,分别写有“和”、“谐”、“校”、“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生![]() 到
到![]() 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用![]() ,
,![]() ,
,![]() ,
,![]() 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下![]() 组随机数:
组随机数:
![]()
由此可以估计,恰好第三次就停止摸球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a,b为常数),
(a,b为常数),
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)在(1)的条件下,![]() 有两个不相等的实根,求b的取值范围;
有两个不相等的实根,求b的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江夏一中高二年级计划假期开展历史类班级研学活动,共有6个名额,分配到历史类5个班级(每个班至少0个名额,所有名额全部分完).
(1)共有多少种分配方案?
(2)6名学生确定后,分成A、B、C、D四个小组,每小组至少一人,共有多少种方法?
(3)6名学生来到武汉火车站.火车站共设有3个“安检”入口,每个入口每次只能进1个旅客,求6人进站的不同方案种数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的普通方程;
的普通方程;
(2)经过点![]() (平面直角坐标系
(平面直角坐标系![]() 中点)作直线
中点)作直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() 恰好为线段
恰好为线段![]() 的三等分点,求直线
的三等分点,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
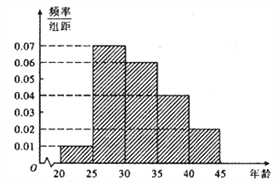
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
 (2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com