
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(Ⅰ)若![]() ,作函数
,作函数![]() 的图像;
的图像;
(Ⅱ)设![]() 在区间[1,2]上的最小值为
在区间[1,2]上的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(Ⅲ)设![]() ,若函数
,若函数![]() 在区间[1,2]上是增函数,求实数
在区间[1,2]上是增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)根据绝对值定义将函数化为分段函数形式,并根据二次函数性质画图(2)先根据a的值分类讨论函数单调性:若![]() ,函数单调递减;若
,函数单调递减;若![]() ,函数单调递增;若
,函数单调递增;若![]() ,函数先减后增;最后求出对应情况下最小值(3)由题意得函数
,函数先减后增;最后求出对应情况下最小值(3)由题意得函数![]() 导函数在[1,2]上恒非负,根据导函数为单调函数得不等式组,解不等式组可得实数
导函数在[1,2]上恒非负,根据导函数为单调函数得不等式组,解不等式组可得实数![]() 的取值范围.
的取值范围.
试题解析:解:(Ⅰ)当![]() 时,
时,![]()
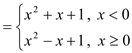 .
.
作图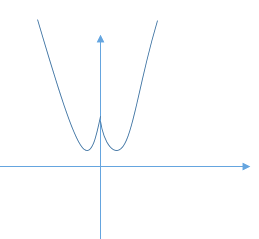
(Ⅱ)当![]() 时,
时,![]() .
.
若![]() ,则
,则![]() 在区间
在区间![]() 上是减函数,
上是减函数,
![]() .
.
若![]() ,则
,则![]() ,
,![]() 图像的对称轴是直线
图像的对称轴是直线![]() .
.
当![]() 时,
时,![]() 在区间
在区间![]() 上是减函数,
上是减函数,![]()
当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上是增函数,
上是增函数,
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 在区间
在区间![]() 上是减函数
上是减函数
![]() .综上可得
.综上可得![]()
 .
.
(Ⅲ)当![]() 时,
时,![]() ,在区间
,在区间![]() 上任取
上任取![]() ,
,![]() ,且
,且![]() ,
,
则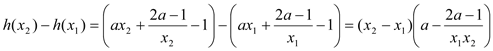
![]() .
.
因为![]() 在区间
在区间![]() 上是增函数,所以
上是增函数,所以![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,
,
当![]() 时,上面的不等式变为
时,上面的不等式变为![]() ,即
,即![]() 时结论成立.
时结论成立.
当![]() 时,
时,![]() ,由
,由![]() 得,
得,![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,由
,由![]() 得,
得,![]() ,解得
,解得![]() ,
,
所以,实数![]() 的取值范围为
的取值范围为![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x)定义域中任意的x1 , x2(x1≠x2)有如下结论
1)f(x1+x2)=f(x1)f(x2)
2)f(x1x2)=f(x1)+f(x2)
3) ![]() >0
>0
4)f( ![]() )<
)< ![]()
5)f( ![]() )>
)> ![]()
6)f(﹣x)=f(x).
当f(x)=lgx时,上述结论正确的序号为 . (注:把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为( )(结果保留一位小数.参考数据:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①原命题为真,它的否命题为假;
②原命题为真,它的 逆命题不一定为真;
③若命题的逆命题为真,则它的否命题一定为真;
④若命题的逆否命题为真,则它的否命题一定为真;
⑤“若 m>1 ,则 mx2-2(m+1)x+m+3>0 的解集为R”的逆命题.
其中真命题是.(把你认为正确命题的序号都填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若对任意m,n∈[﹣1,1],m+n≠0,都有 ![]() .
.
(1)用定义证明函数f(x)在定义域上是增函数;
(2)若 ![]() ,求实数a的取值范围;
,求实数a的取值范围;
(3)若不等式f(x)≤(1﹣2a)t+2对所有和x∈[﹣1,1],a∈[﹣1,1]都恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(3+x)﹣lg(3﹣x)
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并证明;
(3)若f(a)=4,求f(﹣a)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() 上,
上, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]()
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设圆![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于不同的四个点
交于不同的四个点![]() ,求四边形
,求四边形![]() 的面积的最大值及相应的四个点的坐标.
的面积的最大值及相应的四个点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床位每天的租金)不超过10元时,床位可以全部租出;当床位高于10元时,每提高1元,将有3张床位空闲. 为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结帐,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入):
(1)把y表示成x的函数;
(2)试确定,该宾馆将床价定为多少元时,既符合上面的两个条件,又能使净收入高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com