
【题目】偶函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ,不等式
,不等式![]() 在
在![]() 上有且只有200个整数解,则实数
上有且只有200个整数解,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:根据题意得到函数![]() 周期性,结合周期性将问题转化在一个周期
周期性,结合周期性将问题转化在一个周期![]() 内来研究,然后在结合函数图象的对称性将问题转化在
内来研究,然后在结合函数图象的对称性将问题转化在![]() 内研究,最后结合函数
内研究,最后结合函数![]() 在
在![]() 内整数解的个数及图象中的特殊点确定实数
内整数解的个数及图象中的特殊点确定实数![]() 的取值范围.
的取值范围.
详解:由![]() 得函数
得函数![]() 图象的对称轴为
图象的对称轴为![]() ,故
,故![]() ;
;
又![]() ,
,
∴![]() ,
,
∴函数![]() 的周期为
的周期为![]() .
.
作出函数![]() 在一个周期上的图象(如图所示).
在一个周期上的图象(如图所示).
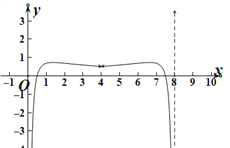
∵函数![]() 为偶函数,且不等式
为偶函数,且不等式![]() 在
在![]() 上有且只有200个整数解,
上有且只有200个整数解,
∴不等式在![]() 上有且只有100个整数解.
上有且只有100个整数解.
∵函数![]() 在
在![]() 内有25个周期,
内有25个周期,
∴函数![]() 在一个周期内有4个整数解,即
在一个周期内有4个整数解,即![]() 在
在![]() 内有4个整数解.
内有4个整数解.
①当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
由图象可得![]() 在一个周期内有7个整数解,不合题意.
在一个周期内有7个整数解,不合题意.
②当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
显然,![]() 在
在![]() 上无整数解,
上无整数解,
∴![]() 在
在![]() 上有4个整数解.
上有4个整数解.
∵![]() 的图象在
的图象在![]() 上关于
上关于![]() 对称,
对称,
∴![]() 在
在![]() 上有2个整数解.
上有2个整数解.
又![]() ,
,
∴![]() ,解得
,解得![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数的上界.已知函数
称为函数的上界.已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() 在
在![]() 上的上界是
上的上界是![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平面![]() 平面
平面![]() 平面
平面![]() ,且
,且![]() 位于
位于![]() 与
与![]() 之间.点
之间.点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() .
.
(2)设AD与CF不平行,且A,B,C,D为定点,![]() 与
与![]() 间的距离为
间的距离为![]() ,
,![]() 与
与![]() 间的距离为h.当
间的距离为h.当![]() 的值是多少时,
的值是多少时,![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假.
(1)过不在平面内的一点,有且只有一个平面与这个平面平行;
(2)过不在平面内的一条直线,有且只有一个平面与这个平面平行;
(3)给定两个平行平面中一个平面内的一条直线,则在另一个平面内有且只有一条直线与这条直线平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com