
【题目】已知点M(x,y)满足![]()
(1)求点M的轨迹E的方程;
(2)设过点N(﹣1,0)的直线l与曲线E交于A,B两点,若△OAB的面积为![]() (O为坐标原点).求直线l的方程.
(O为坐标原点).求直线l的方程.
科目:高中数学 来源: 题型:
【题目】旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为15000元.旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数不超过35人时,飞机票每张收费800元;若旅游团的人数多于35人,则给予优惠,每多1人,机票费每张减少10元,但旅游团的人数最多有60人.设旅行团的人数为![]() 人,飞机票价格为
人,飞机票价格为![]() 元,旅行社的利润为
元,旅行社的利润为![]() 元.
元.
(1)写出飞机票价格![]() 元与旅行团人数
元与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当旅游团的人数![]() 为多少时,旅行社可获得最大利润?求出最大利润.
为多少时,旅行社可获得最大利润?求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①函数![]() 的最大值为1;
的最大值为1;
②“若![]() ,则
,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
③若![]() 为锐角三角形,则有
为锐角三角形,则有![]() ;
;
④“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件.
内单调递增”的充分必要条件.
其中所有正确命题的序号为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(I)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(II)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励. 现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销售量不低于10万件的概率.
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为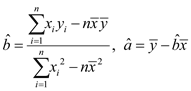 . 参考数据:
. 参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com