
【题目】在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() .向量
.向量![]() ,
,![]() ,且
,且![]()
(1)若![]() ,求角
,求角![]() 的值;
的值;
(2)求角![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:椭圆![]() 的焦点在
的焦点在![]() 轴上,左焦点
轴上,左焦点![]() 与短轴两顶点围成面积为
与短轴两顶点围成面积为![]() 的等腰直角三角形,直线
的等腰直角三角形,直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() (
(![]() 、
、![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 为椭圆与
为椭圆与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 的方程;
的方程;
(3)对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种大型商品,![]() 、
、![]() 两地都有出售,且价格相同,现
两地都有出售,且价格相同,现![]() 地的居民从
地的居民从![]() 、
、![]() 两地之一购得商品后回运的运费是:
两地之一购得商品后回运的运费是:![]() 地每公里的运费是
地每公里的运费是![]() 地运费的
地运费的![]() 倍,已知
倍,已知![]() 、
、![]() 两地相距
两地相距![]() ,居民选择
,居民选择![]() 或
或![]() 地购买这种商品的标准是:包括运费和价格的总费用较低.
地购买这种商品的标准是:包括运费和价格的总费用较低.
(1)求![]() 地的居民选择
地的居民选择![]() 地或
地或![]() 地购物总费用相等时,点
地购物总费用相等时,点![]() 所在曲线的形状;
所在曲线的形状;
(2)指出上述曲线内、曲线外的居民应如何选择购货地点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 且
且![]() ,
,![]() .
.
(1)若函数f(x)与g(x)有相同的极值点(极值点是指函数取极值时对应的自变量的值),求k的值;
(2)当m>0,k = 0时,求证:函数![]() 有两个不同的零点;
有两个不同的零点;
(3)若![]() ,记函数
,记函数![]() ,若
,若![]() ,使
,使![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆![]() 经过坐标原点和点
经过坐标原点和点![]() ,且与直线
,且与直线![]() 相切, 从圆
相切, 从圆![]() 外一点
外一点![]() 向该圆引切线
向该圆引切线![]() ,
,![]() 为切点,
为切点,
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,且
,且![]() , 试判断点
, 试判断点![]() 是否总在某一定直线
是否总在某一定直线![]() 上,若是,求出
上,若是,求出![]() 的方程;若不是,请说明理由;
的方程;若不是,请说明理由;
(Ⅲ)若(Ⅱ)中直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 是直线
是直线![]() 上两动点,且以
上两动点,且以![]() 为直径的圆
为直径的圆![]() 过点
过点![]() ,圆
,圆![]() 是否过定点?证明你的结论.
是否过定点?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关平面向量分解定理的四个命题:
(1)一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基;
(2)一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基;
(3)平面向量的基向量可能互相垂直;
(4)一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.
其中正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有除颜色外形状大小完全相同的6个小球,其中有4个编号为1,2, 3, 4的红球,2个编号为A、B的黑球,现从中任取2个小球.;
(1)求所取2个小球都是红球的概率;
(2)求所取的2个小球颜色不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 满足:
满足:![]() ,且
,且![]() 成等比数列,
成等比数列,![]() 成等差数列.
成等差数列.
(1)行列式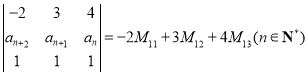 ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(2)在(1)的条件下,若![]() 不是常数列,
不是常数列,![]() 是等比数列,
是等比数列,
①求![]() 和
和![]() 的通项公式;
的通项公式;
②设![]() 是正整数,若存在正整数
是正整数,若存在正整数![]() ,使得
,使得![]() 成等差数列,求
成等差数列,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com