
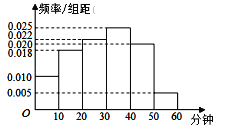
����Ŀ������һ��Ϊ�о�ѧ�������������������������ʱ��Ĺ�ϵ����ȡ��У200��ѧ���Ŀ�����������ƽ��ÿ���˶���ʱ�䣨��λ�����ӣ����е��飬���ռ������ݷֳ�![]() ��
��![]() ���飬������Ƶ�ʷֲ�ֱ��ͼ����ͼ�������վ�������������ʱ�䲻����40���ӵ�ѧ������Ϊ������������ꡱ��
���飬������Ƶ�ʷֲ�ֱ��ͼ����ͼ�������վ�������������ʱ�䲻����40���ӵ�ѧ������Ϊ������������ꡱ��
������������� | ����������� | �ϼ� | |
�� |
| ||
Ů |
| ||
�ϼ� |
��1�������ֱ��ͼ�е�������д�����![]() ����������ͨ�������ж��Ƿ����ڷ�����ĸ��ʲ�����
����������ͨ�������ж��Ƿ����ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ������������ꡱ���Ա��йأ�
��ǰ������Ϊ������������ꡱ���Ա��йأ�
��2����![]() �������в�ȡ�ֲ��������ȡ6�ˣ��ٴ���6��ѧ���������ȡ2�˲μ�����֪ʶ�ʾ����飬����2����һ�����ԡ�����������ꡱ��һ�����ԡ�������������ꡱ�ĸ��ʣ�
�������в�ȡ�ֲ��������ȡ6�ˣ��ٴ���6��ѧ���������ȡ2�˲μ�����֪ʶ�ʾ����飬����2����һ�����ԡ�����������ꡱ��һ�����ԡ�������������ꡱ�ĸ��ʣ�
���ο���ʽ�룺![]()
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
���𰸡���1�����ܣ���2��![]() .
.
��������������(1)����Ƶ�ʷֲ�ֱ��ͼ,�����Ӧ������,��д![]() ������,����۲�ֵ
������,����۲�ֵ![]() ,���������ó�����;
,������������;
(2)���ݷֲ�����Լ��оٷ������Ӧ�Ļ����¼���,�����Ӧ�ĸ���ֵ.
��⣺��1��������á�����������ꡱ������200��[��0.02+0.005����10]=50��
�������Ϊ150��
�����������£�
������������� | ����������� | �ϼ� | |
�� | 60 | 30 | 90 |
Ů | 90 | 20 | 110 |
�ϼ� | 150 | 50 | 200 |
��k2=![]() =
=![]() ��6.060��6.635��
��6.060��6.635��
���ڷ�����ĸ��ʲ�����0.01��ǰ����û�����ɣ����ܣ���Ϊ������������ꡱ���Ա��й�.
��2����������[0��10����[40��50���ֱ���20�ˣ�40�ˣ�
���ȡ�ֲ������[0��10����ȡ������Ϊ��![]() �ˣ�
�ˣ�
��[40��50����ȡ������Ϊ��![]() �ˣ�
�ˣ�
[0��10����ȡ����ΪA��B����[40��50����ȡ����Ϊa��b��c��d��
����6���������ȡ2�˵����Ϊ��AB��Aa��Ab��Ac��Ad��Ba��Bb��Bc��Bd��ab��ac��ad��bc��bd��cd��15�֣�
2����һ�����ԡ�����������ꡱ��һ�����ԡ�������������ꡱ���У�Aa��Ab��Ac��Ad��Ba��Bb��Bc��Bd��8�֣�
��![]() ��
��


 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��Բ
��Բ![]() .
.
(1)��ֱ��![]() ����
����![]() ����Բ��
����Բ��![]() �ľ���Ϊ1����ֱ��
�ľ���Ϊ1����ֱ��![]() �ķ��̣�
�ķ��̣�
(2)�����![]() ��ֱ��
��ֱ��![]() ��Բ
��Բ![]() ����
����![]() ���㣬��
���㣬��![]() ʱ�������߶�
ʱ�������߶�![]() Ϊֱ����Բ
Ϊֱ����Բ![]() �ķ��̣�
�ķ��̣�
(3)��ֱ��![]() ��Բ
��Բ![]() ����
����![]() ���㣬�Ƿ����ʵ��
���㣬�Ƿ����ʵ��![]() ��ʹ�ù���
��ʹ�ù���![]() ��ֱ��
��ֱ��![]() ��ֱƽ����
��ֱƽ����![]() �������ڣ����ʵ��
�������ڣ����ʵ��![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ���ĺ���
���ĺ���![]() ��������㣺������
��������㣺������![]() �����ڳ���
�����ڳ���![]() ������
������![]() ���������
���������![]() ��
��![]() �����н纯��������
�����н纯��������![]() ��Ϊ����
��Ϊ����![]() ���Ͻ�����֪����
���Ͻ�����֪����![]() ��
��
��1����![]() ʱ������
ʱ������![]() ��
��![]() ����ֵ���жϺ���
����ֵ���жϺ���![]() ��
��![]() ���Ƿ�Ϊ�н纯������˵�����ɣ�
���Ƿ�Ϊ�н纯������˵�����ɣ�
��2��������![]() ��
��![]() ������4Ϊ�Ͻ���н纯������ʵ��
������4Ϊ�Ͻ���н纯������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�������㷨ͳ�ڡ������������⣺��Զ��ΡΡ���߲㣬����㱶�������������ٰ�ʮһ�����ʼ�ͷ��յ�ƣ�����˼�ǣ�һ��7����������381յ�ƣ������������е���һ���������һ�������2���������Ķ��㹲�еƣ� ��
A. 1յ B. 3յ C. 5յ D. 9յ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���ڴ�ֱ��ˮƽ����ABC��ǽ��ǰ�ĵ�A���������ѵ������֪��A��ǽ��ľ���ΪAB��ijĿ���P��ǽ���ϵ�����CM�ƶ�������Ϊ��ȷ��Ŀ���P��������ɵ�A�۲��P�����ǦȵĴ�С����AB=15m��AC=25m����BCM=30�㣬��tan�ȵ����ֵ�� �� �����Ǧ�Ϊֱ��AP��ƽ��ABC���ɽǣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ԲC�� ![]() ��a��b��0������ֱ��l����ԲCֻ��һ��������P���ҵ�P�ڵ�һ���ޣ�
��a��b��0������ֱ��l����ԲCֻ��һ��������P���ҵ�P�ڵ�һ���ޣ� 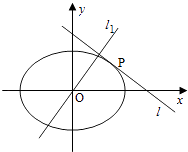
��1����ֱ֪��l��б��Ϊk����a��b��k��ʾ��P�����ꣻ
��2������ԭ��O��ֱ��l1��l��ֱ��֤������P��ֱ��l1�ľ�������ֵΪa��b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������������ǣ� ��
A. �����ں����Ķ����ж�ij�����Ƿ�Ϊ���ں���
B. ��![]() �������κ�һ��С6��ż����������������֮��
�������κ�һ��С6��ż����������������֮��
C. ƽ���ڲ����ߵ�3����ȷ��һ��Բ���ɴ˲���ռ䲻�����4����ȷ��һ����
D. ��֪![]() Ϊ���㣬������P����
Ϊ���㣬������P����![]() ������
������![]() �����������
Ϊ�����������![]() �Ĺ켣Ϊ��Բ
�Ĺ켣Ϊ��Բ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ־Ը��Э����6����ͬѧ��4��Ůͬѧ������10��ͬѧ�У�3��ͬѧ������ѧѧԺ������7��ͬѧ������������ѧ������������ͬ���߸�ѧԺ���ִ���10��ͬѧ�����ѡȡ3��ͬѧ����ϣ��Сѧ����֧�̻��ÿλͬѧ��ѡ���Ŀ�������ͬ����
��1����ѡ����3��ͬѧ�����Ի�����ͬѧԺ�ĸ��ʣ�
��2����XΪѡ����3��ͬѧ��Ůͬѧ�����������������X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���賣��a��0������f��x��= ![]() ��
��
��1����a=4������y=f��x���ķ�����y=f��1��x����
��2������a�IJ�ͬȡֵ�����ۺ���y=f��x������ż�ԣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com