
【题目】如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥ AB,M是EC上的点(不与端点重合),F为DA上的点,N为BE的中点.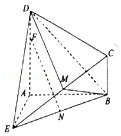
(Ⅰ)若M是EC的中点,AF=3FD,求证:FN∥平面MBD;
(Ⅱ)若平面MBD与平面ABD所成角(锐角)的余弦值为 ![]() ,试确定点M在EC上的位置.
,试确定点M在EC上的位置.
【答案】(Ⅰ)证明:如图, 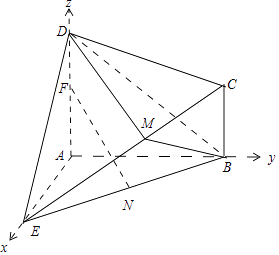
∵DA⊥平面EAB,∴DA⊥AE,DA⊥AB,又EA⊥AB,
∴以A为原点,分别以AE、AB、AD所在直线为x、y、z轴建立空间直角坐标系,
设CB=4,由CB∥DA,EA=DA=AB=2CB,N为BE的中点,M是EC的中点,AF=3FD,
得F(0,0,6),N(4,4,0),M(4,4,2),B(0,8,0),D(0,0,8),
C(0,8,4),E(8,0,0).
∴ ![]() ,
, ![]() ,
, ![]() .
.
设平面MBD的一个法向量为 ![]() ,
,
由  ,取z=1,得
,取z=1,得 ![]() .
.
∵ ![]() =
= ![]() ,∴
,∴ ![]() ,则FN∥平面MBD;
,则FN∥平面MBD;
(Ⅱ)解:设 ![]() ,M(x1 , y1 , z1),
,M(x1 , y1 , z1),
则 ![]() =(x1 , y1﹣8,z1﹣4),
=(x1 , y1﹣8,z1﹣4), ![]() ,
,
∴(x1 , y1﹣8,z1﹣4)=(8λ,﹣8λ,﹣4λ),
∴ 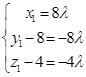 ,得M(8λ,8﹣8λ,4﹣4λ),
,得M(8λ,8﹣8λ,4﹣4λ),
∴ ![]() .
.
设平面BDM的一个法向量为 ![]() ,
,
由 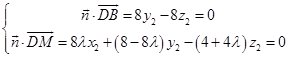 ,取z2=1,得
,取z2=1,得 ![]() .
.
平面ABD的一个法向量为 ![]() ,
,
由|cos< ![]() >|=|
>|=| ![]() |=|
|=| 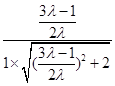 |=
|= ![]() ,得8λ2﹣6λ+1=0,
,得8λ2﹣6λ+1=0,
解得 ![]() 或
或 ![]() .
.
∵平面MBD与平面ABD所成角(锐角)的余弦值为 ![]() ,∴
,∴ ![]() ,即M为EC中点.
,即M为EC中点.
【解析】(Ⅰ)由题意可得AE、AB、AD两两垂直,以A为原点,分别以AE、AB、AD所在直线为x、y、z轴建立空间直角坐标系,求出 ![]() 的坐标,再求出平面MBD的一个法向量
的坐标,再求出平面MBD的一个法向量 ![]() ,由
,由 ![]() 可得FN∥平面MBD;(Ⅱ)设
可得FN∥平面MBD;(Ⅱ)设 ![]() ,把M的坐标用λ表示,求出平面BDM的一个法向量,再求出平面ABD的一个法向量,由两法向量所成角的余弦值的绝对值为
,把M的坐标用λ表示,求出平面BDM的一个法向量,再求出平面ABD的一个法向量,由两法向量所成角的余弦值的绝对值为 ![]() 求得λ值,则答案可求.
求得λ值,则答案可求.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的分别为a,b,c,且acosB=(3c﹣b)cosA.
(1)若asinB=2 ![]() ,求b;
,求b;
(2)若a=2 ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)如表所示是某市最近5年个人年平均收入表节选.求y关于x的回归直线方程,并估计第6年该市的个人年平均收入(保留三位有效数字).
年份x | 1 | 2 | 3 | 4 | 5 |
收入y(千元) | 21 | 24 | 27 | 29 | 31 |
其中![]() ,
,![]() ,
,![]() 附1:
附1:![]() =
= ![]() ,
,![]() =
=![]() ﹣
﹣![]()
![]()
(Ⅱ)下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表:
受培时间一年以上 | 受培时间不足一年 | 总计 | |
收入不低于平均值 | 60 | 20 | |
收入低于平均值 | 10 | 20 | |
总计 | 100 |
完成上表,并回答:能否在犯错概率不超过0.05的前提下认为“收入与接受培训时间有关系”.
附2:
P(K2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
附3:
K2=![]() .(n=a+b+c+d)
.(n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C对应的边分别为a、b、c,已知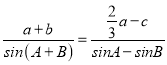 .
.
(1)求cosB的值;
(2)若b=8,cos2A﹣3cos(B+C)=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增大,下表是该地一农业银行连续五年的储蓄存款(年底余额),如下表:

为了研究方便,工作人员将上表的数据进行了处理,![]() ,得到下表:
,得到下表:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)用所求回归方程预测,到2020年底,该地储蓄存款额大约可达多少?
(附:线性回归方程:![]() ,
,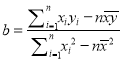 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x3与g(x)=x3﹣ax的图象上存在关于x轴的对称点,则实数a的取值范围为( )
A.(﹣∞,e)
B.(﹣∞,e]
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() 中,底面
中,底面![]() 的边长为2,侧棱长为4,
的边长为2,侧棱长为4,![]() 是线段
是线段![]() 上一点,
上一点,![]() 是线段
是线段![]() 的中点,
的中点,![]() 为
为![]() 的中点.以
的中点.以![]() 为正交基底,建立如图所示的空间直角坐标系
为正交基底,建立如图所示的空间直角坐标系![]() .
.

(1)若![]() ,求直线
,求直线![]() 和平面
和平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若二面角![]() 的正弦值为
的正弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com